Cho a > 1. Biết khi a = a 0 thì bất phương trình x a ≤ a x đúng với mọi x ∈ 1 ; + ∞ . Mệnh đề nào dưới đây đúng?
A. 1 < a 0 < 2
B. e < a 0 < e 2
C. 2 < a 0 < 3
D. e 2 < a 0 < e 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

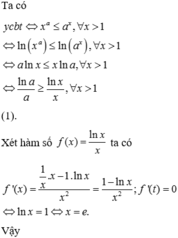
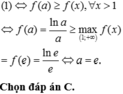

Đáp án C.
Áp dụng lý thuyết về “ Dấu của tam thức bậc hai” ta thấy đáp án C là đáp án đúng.

Đáp án B
Đặt 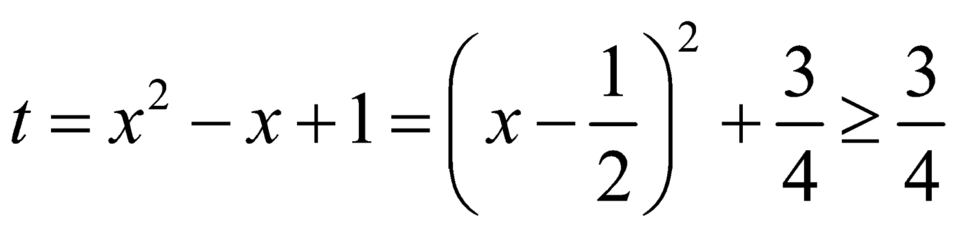
Ta có:
![]()
![]()
Đặt ![]() .
.
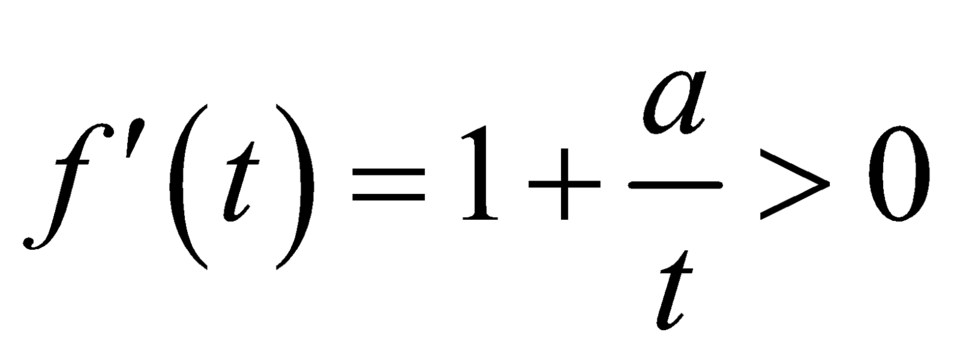
![]() là hàm số đồng biến trên
là hàm số đồng biến trên 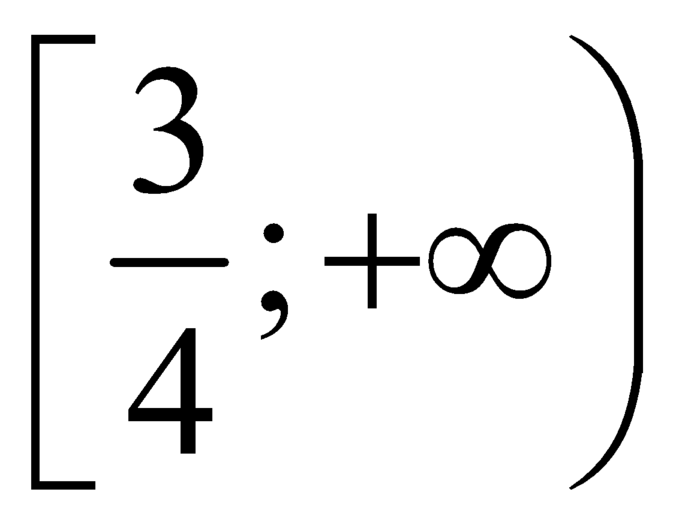 .
.
Khi đó 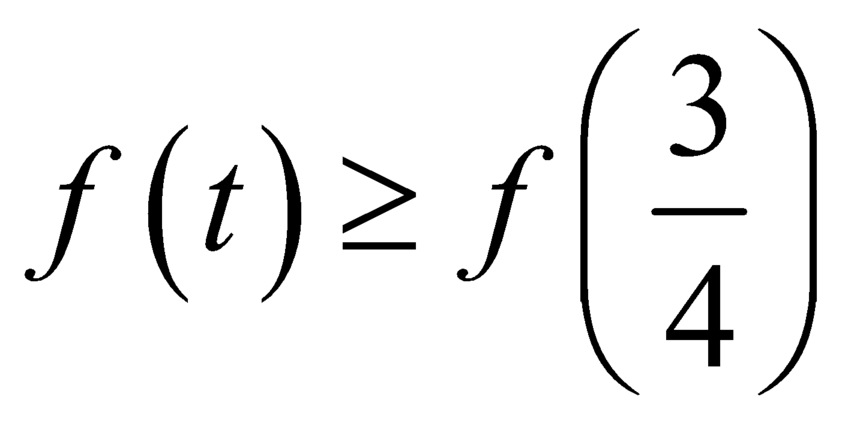
![]()
![]()
![]()

Đặt t = 3 x > 0 . Bất phương trình đã cho trở thành
a t 2 + 9 a - 1 t + a - 1 > 0 ⇔ a > 9 t t 2 + 9 t + 1
Bất phương trình đã cho nghiệm đúng với mọi x khi và chỉ khi a > m a x t ∈ 0 ; + ∞ f t với f t = 9 t t 2 + 9 t + 1
Ta có f ' t = - 9 t 2 t 2 + 9 t + 1 2 < 0 ; ∀ t > 0 ⇒ f t là hàm nghịch biến trên 0 ; + ∞ .
Suy ra f(t) < f(0) = 1
Do đó 9 t t 2 + 9 t + 1 < 1 ; ∀ t > 0 nên các giá trị của a cần tìm là a ≥ 1
Đáp án B

Chọn đáp án C

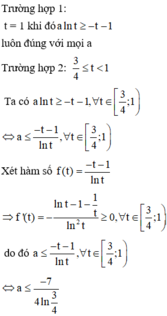
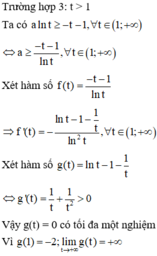
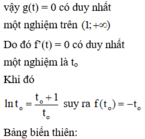
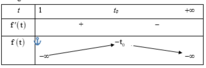

Vậy số thực a thỏa mãn yêu cầu bài toán là: a ∈ ( 6 ; 7 ]

Đáp án A.
Đặt t = x 2 − x + 1 = x − 1 2 2 + 3 4 ≥ 3 4
Khi đó BPT trở thành
f t = t + 1 + a ln t ≥ 0
Ta có: f ' t = + ∞ ; f 3 4 = 3 4 + a ln 3 4
Với a > 0 ⇒ f t đồng biến trên
3 4 ; + ∞ ⇒ f t ≥ 0 ∀ t ∈ 3 4 ; + ∞ ⇔ M i n 3 4 ; + ∞ f t = 7 4 + a
⇔ a ln 3 4 ≥ − 7 4 ⇔ a ≤ − 7 4 ln 3 4 ≈ 6 , 08.
Vì đề bài yêu cầu tìm số thực lớn nhất
nên suy ra a ∈ 6 ; 7 .