giúp mik với

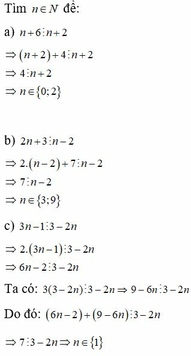
\(a,2.\left|x+1\right|-3=5\)

\(\Rightarrow2.\left|x+1\right|=5+3\)

\(\Rightarrow2.\left|x+1\right|=8\)

\(\Rightarrow\left|x+1\right|=8:2\)

\(\Rightarrow\left|x+1\right|=4\)

\(\Rightarrow\orbr{\begin{cases}x+1=4\\x+1=-4\end{cases}}\Rightarrow\orbr{\begin{cases}x=3\\x=-5\end{cases}}\)

Vậy : x = 3 hoặc x = -5

b) Để A có giá trị nguyên thì n + 1 \(⋮\)n - 2

Ta có : n + 1 = ( n - 2 ) + 3

=> n + 1 \(⋮\)n - 2

khi ( n - 2 ) + 3 \(⋮\) n - 2

=> 3 \(⋮\)n - 2

=> n - 2 \(\in\)Ư ( 3 ) = { 1 ; -1 ; 3 ; -3 }

Với n - 2 = 1 => n = 3

Với n - 2 = -1 => n = 1

Với n - 2 = 3 => n = 5

Với n - 2 = -3 => n = -1 

Vậy : n \(\in\){ 3 ; 1 ; 5 ; -1 }

Bài 3:

a: \(35-12n⋮n\)

\(\Leftrightarrow n\in\left\{1;5;7;35\right\}\)

b: \(n+13⋮n+5\)

\(\Leftrightarrow n+5\in\left\{1;-1;2;-2;4;-4;8;-8\right\}\)

hay \(n\in\left\{-4;-6;-3;-7;-1;-9;3;-13\right\}\)

 12 nha

Chắc Không Vậy

a, n+6 ⋮ n+2 => (n+2)+4 ⋮ n+2

=> 4 ⋮ n+2

=> n ∈ {0;2}

b, 2n+3 ⋮ n - 2

=> 2.(n - 2)+7 ⋮ n - 2

=> 7 ⋮ n - 2

=> n ∈ {3;9}

c, 3n - 1 ⋮ 3 - 2n

=> 2.(3n - 1) ⋮ 3 - 2n

=> 6n - 2 ⋮ 3 - 2n

Ta có: 3(3 - 2n) ⋮ 3 - 2n => 9 - 6n ⋮ 3 - 2n

Do đó: (6n - 2)+(9 - 6n) ⋮ 3 - 2n

=> 7 ⋮ 3 - 2n => n ∈ {1}

\(n^3-2⋮n-2\)

=>\(n^3-8+6⋮n-2\)

=>\(6⋮n-2\)

=>\(n-2\in\left\{1;-1;2;-2;3;-3;6;-6\right\}\)

=>\(n\in\left\{3;1;4;0;5;-1;8;-4\right\}\)

\(a=lim\dfrac{\left(\dfrac{2}{6}\right)^n+1-\dfrac{1}{4}\left(\dfrac{4}{6}\right)^n}{\left(\dfrac{3}{6}\right)^n+6}=\dfrac{1}{6}\)

\(b=\lim\dfrac{\left(n+1\right)^2}{3n^2+4}=\lim\dfrac{n^2+2n+1}{3n^2+4}=\lim\dfrac{1+\dfrac{2}{n}+\dfrac{1}{n^2}}{3+\dfrac{4}{n^2}}=\dfrac{1}{3}\)

\(c=\lim\dfrac{n\left(n+1\right)}{2\left(n^2-3\right)}=\lim\dfrac{n^2+n}{2n^2-6}=\lim\dfrac{1+\dfrac{1}{n}}{2-\dfrac{6}{n^2}}=\dfrac{1}{2}\)

\(d=\lim\left[1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{n}-\dfrac{1}{n+1}\right]=\lim\left[1-\dfrac{1}{n+1}\right]=1\)

\(e=\lim\dfrac{1}{2}\left[1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{2n-1}-\dfrac{1}{2n+1}\right]\)

\(=\lim\dfrac{1}{2}\left[1-\dfrac{1}{2n+1}\right]=\dfrac{1}{2}\)

a, \(\frac{2n+2}{2n-1}=\frac{2n-1+3}{2n-1}=1+\frac{3}{2n-1}\)

Để \(2n+2⋮2n-1\text{thì}2n-1\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)

Xét bảng ( tự xét nha )

KL

b, \(\frac{2n-5}{n+3}=\frac{2\left(n+3\right)-11}{n+3}=2-\frac{11}{n+3}\)

\(\text{Để}2n-5⋮n+3\text{thì}n+3\inƯ\left(11\right)=\left\{\pm1;\pm11\right\}\)

Xét bảng ( tự xét nha )

KL

nhìn cậu làm,hình như sai thì phải