Cho tứ diện ABCD. Gọi G1 và G2 lần lượt là trọng tâm các tam giác BCD và ACD. Trong các khẳng định sau, khẳng định nào sai?
A. G 1 G 2 = 2 3 A B
B. G 1 G 2 / / A B D
C. G 1 G 2 / / A B C
D. B G 1 , A G 2 và CD đồng qui
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

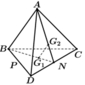
Gọi N là trung điểm của CD
● Khi đó A, G 2 , N thẳng hàng và B, G 1 , N thẳng hàng.
Do đó, B G 1 , A G 2 và CD đồng quy
![]() Áp dụng định lí Talet đảo, suy ra
Áp dụng định lí Talet đảo, suy ra
![]()
![]()
Do đó D sai. Chọn D.

Khẳng định thứ (III) kia chính xác là gì nhỉ? Chắc chắn 30G là ko hợp lý rồi

Đáp án A.
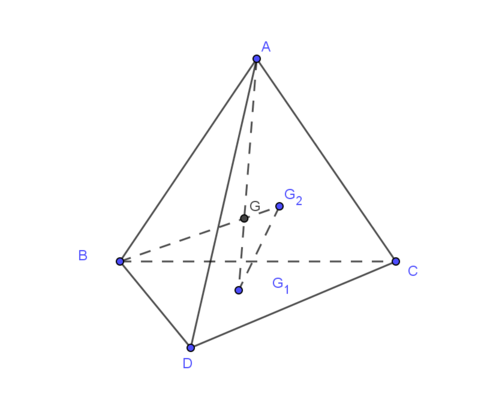
Hình vẽ dễ thấy tính song song là: G 1 G 2 ∥ A B
Chứng minh
Vì G G 1 G A = G G 2 G B = 1 4 ⇒ G 1 G 2 ∥ A B

Đáp án C.
+ Gọi G 0 là trọng tâm tam giác BCD=> G B ⇀ + G C ⇀ + G D ⇀ = 3 G G 0 ⇀
=>
G
A
⇀
+
G
B
⇀
+
G
C
⇀
+
G
D
⇀
=
0
⇀
![]()
=> A, G, G 0 thẳng hàng ⇒ G 0 = G A
+ Có A, G,
G
A
thẳng hàng mà ![]()