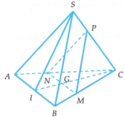
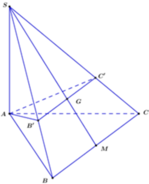
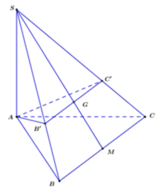
Cho hình chóp S . A B C . Bên trong tam giác ABC ta lấy một điểm O bất kỳ. Từ O ta dựng các đường thẳng lần lượt song song với SA, SB, SC và cắt các mặt phẳng S B C , S C A , S A B theo thứ tự tại các điểm A’ , B’ , C’ . Tính tổng tỉ số T = O A ' S A + O B ' S B + O C ' S C .
A. T = 3
B. T = 3 4
C. T = 1
D. T = 1 3

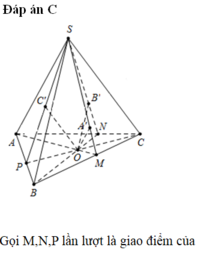

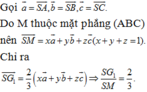
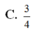
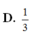

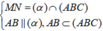
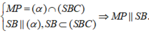
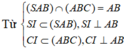
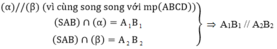

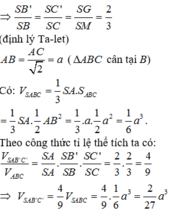
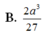
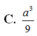
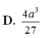


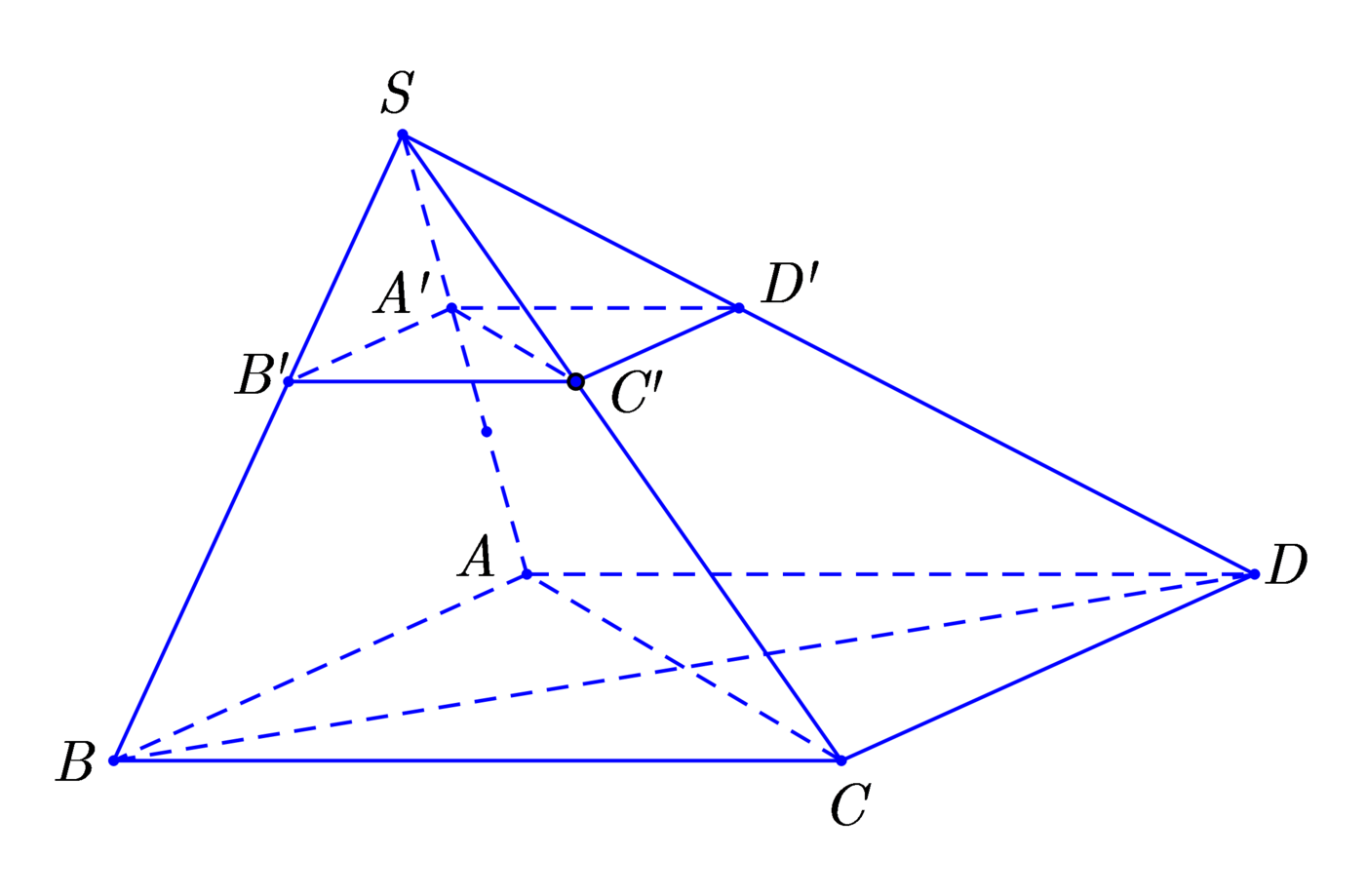
Đáp án C
Gọi M,N,P lần lượt là giao điểm của OA, OB, OC với cạnh BC, CA, AB.
Vì O B ' / / S A ⇒ O A ' S A = O M A M (Định lí Thalet).
Tương tự, ta có O B ' S B = O N B N ' ; O C ' S C = O P P C ⇒ T = O M A M + O N B N + O P P C .
Với O là trọng tâm của tam giác ABC ⇒ M , N , P lần lượt là trung điểm của BC, CA, AB
⇒ O M A M = O N B N = O P C P = 1 3 . Vậy tổng tỉ số T = O A ' S A + O B ' S B + O C ' S C = 1.
Chú ý: Bản chất bài toán là yêu cầu chứng minh O M A M + O N B N + O P P C = 1. Tuy nhiên với tinh thần trắc nghiệm ta sẽ chuẩn hóa với O là trọng tâm tam giác ABC.