Cho tam giác ABC cân tại A,đường trung tuyến AM.Đường trung trực ủa AC cắt đường thẳng AM ở D.Chứng minh rằng DA=DB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì ∆ABC cân tại A, AM là đường trung tuyến ứng với cạnh đáy BC nên AM cũng là đường trung trực của BC.
Vì D là giao điểm của các đường trung trực AC và BC nên D thuộc đường trung trực của AB.
Theo tính chất đường trung trực, ta có:
DA = DB.

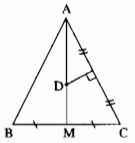
∆ABC cân tại A, AM là đường trung tuyến ứng với cạnh đáy BC nên AM cũng là đường trung trực của BC.
D là giao điểm của các đường trung trực AC và BC nên D thuộc trung trực của AB.
Vậy DA = DB (tính chất đường trung trực).

Ta có DA=DC( vì điểm D nằm trên đường trung trực của AC) (1)
Ta có \(AM⊥BC\), vì trong tam giác cân, đường trung tuyến đồng thời là đường phân giác
=> \(\widehat{AMB}=\widehat{AMC}=90\) độ hay \(\widehat{DMB}=\widehat{DMC}=90\) độ
=> Tam giác DMB và tam giác DMC vuông tại M
Xét tam giác DMB và tam giác DMC có
BM=MC( vì AM là đường trung tuyến của tam giác ABC)
Cạnh DM chung
=> Tam giác DMB=tam giác DMC( 2 cạnh góc vuông)
=>DB=DC (2)
Từ (1) và (2) => DA=DB
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)

a: Xét ΔAMB và ΔAMC có
AM chung
AB=AC
MB=MC
=>ΔAMB=ΔAMC
b: Xét ΔDMB vuông tạiM và ΔDMC vuông tại M có
DM chung
MB=MC
=>ΔDMB=ΔDMC
c: ΔDMB=ΔDMC
=>DB=DC
D nằm trên trung trực của AC
=>DA=DC=DB


a) Chứng minh:BEM=CFM
Xét tam giác BEM và tam giác CFM, có:
- góc BEM = góc CFM = 90 độ (do ME vuông góc AB; MF vuông góc AC)
- MB = MC (AM là trung tuyến, trung trực của tam giác ABC)
- góc B = góc C (do tam giác ABC cân tại A)
=> tam giác BEM và tam giác CFM (tam giác vuông có cạnh huyền, góc nhọn bằng nhau) (đpcm)
b)Chứng minh: AM là trung trực của EF
Gọi I là điểm giao nhau của AM và EF
Xét tam giác AEI và tam giác AFI, có
- AE = AF (do AE = AB - EB, AF = AC - FC; mà AB = AC co tam giác ABC cân, EB = FC do tam giác BEM = tam giác CFM)
- góc EAI = góc FAI (do AM là trung tuyến, trung trực, phân giác của tam giác cân ABC)
- cạnh AI chung
=> tam giác AEI = tam giác AFI
=> AR = AF =>tam giác AEF cân tại F (1)
Thêm nữa: IE = IF => I là trung điểm của EF (2)
Từ (1) và (2) => AI là trung tuyến của tam giác cân AEF, và cũng là là trung trực của tam giác AEF
=> AI vuông góc EF tại I
mà A,I,M thẳng hàng
=> AM là trung trực của EF
c) Từ B kẻ đường thẳng vuông góc với AB tại B,từ C kẻ đường thẳng vuông góc với AC tại C,hai đường thẳng này cắt nhau tại D.Chứng minh rằng ba điểm A,M,D thẳng hàng
Xét tam giác vuông ABD và tam giác vuông ACD, có
- AB = AC
- BAD = CAD
- AD chung
=> tam giác vuông ABD = tam giác vuông ACD
=> DB = DC
=> tam giác DBC cân tại D
mà M là trung điểm BC
=> DM là trung trực, trung tuyến, phân giác của tam giác cân DBC
=> góc BMD = 90 độ
Ta có góc AMB = 90 độ; góc BMD = 90 độ
=> góc AMB + góc BMD = 90 độ + 90 độ = 180 độ
=> 3 điểm A,M,D thẳng hàng
a) do tam giac abc can tai a (gt)
-> ab=ac(t/c)
-> goc b=goc c(t/c)
theo gt am la trung tuyen
->m la trung diem cua bc
->bm=cm=bc/2 (t/c)
xet tam giac bem va tam giac cem co:
goc bem=cem=90 do
goc b=goc c (cmt)
bm=cm (cmt)
-> tam giac bem = tam giac cem (ch-gn)
cau a cua co giao lan thieu

a: Sửa đề ΔAMC
Xét ΔAMC và ΔDMB có
góc MCA=góc MBD
MC=MB
góc AMC=góc DMB
=>ΔAMC=ΔDMB
b: ΔAMC=ΔDMB
=>AC=BD
=>BD=AB
c: Xét ΔBAD có
BM,DP là trung tuyến
BM cắt DP tại O
=>O là trọng tâm
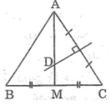

Vì D nằm trên đường trung trực của AC
nên DA=DC(1)
Xét ΔDBC có
DM là đường cao
DM là đường trung tuyến
Do đó;ΔDBC cân tại D
=>DB=DC(2)
Từ (1) và (2) suy ra DA=DB
Vì tam giac ABC cân tại A
Mà AM là đường trung tuyến ứng với cạnh đáy BC
=> AM cũng là đường trung trực của BC.
Có D là giao điểm của các đường tt AC và BC
=> D thuộc đường trung trực của AB.
Theo tính chất đường trung trực , có:
=>DA = DB.