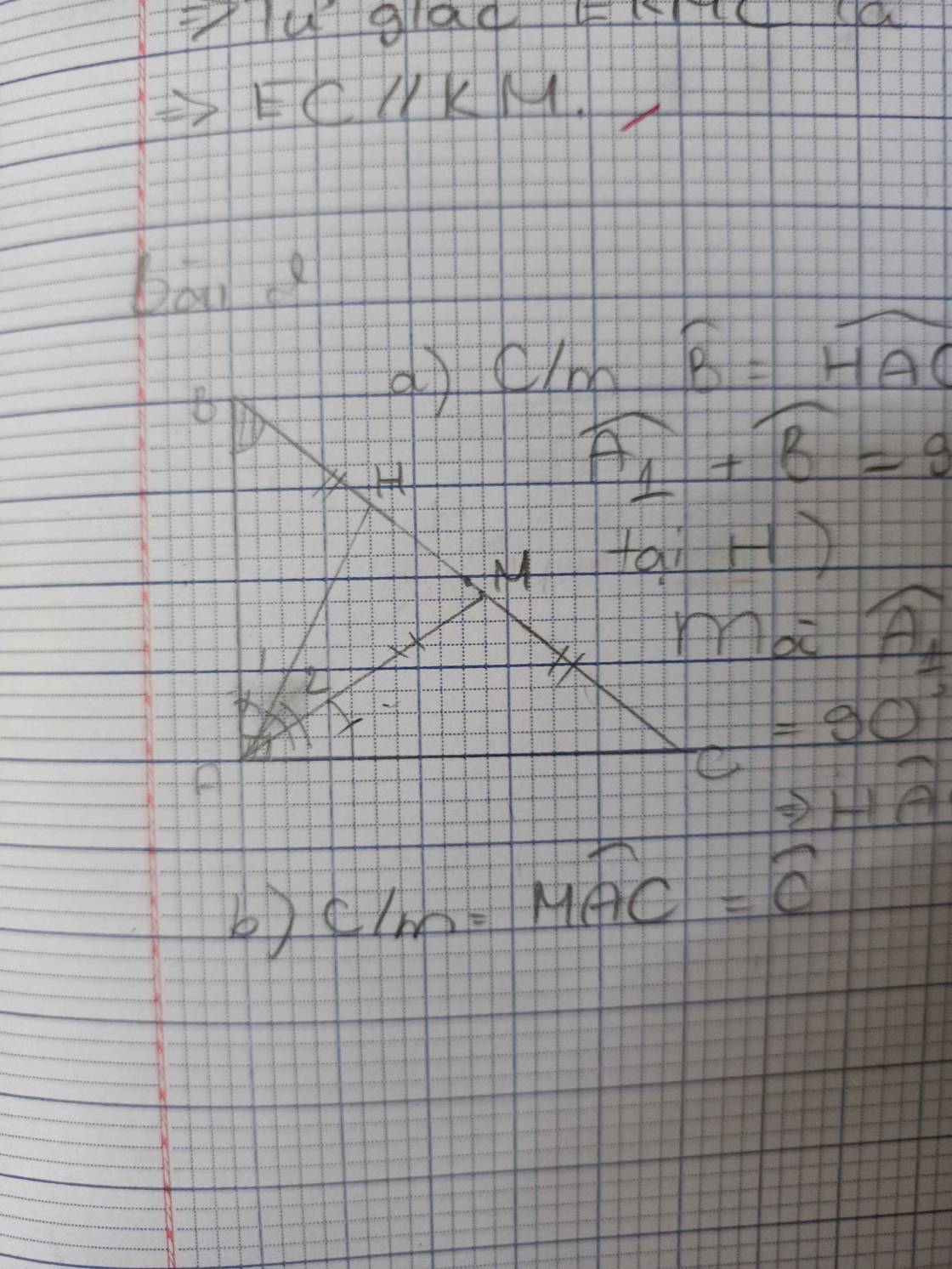a.

Do E là trung điểm AB, M là trung điểm BC

\(\Rightarrow\) EM là đường trung bình tam giác ABC

\(\Rightarrow EM||AC\)

\(\Rightarrow\widehat{MAC}=\widehat{AME}\) (so le trong) (1)

Trong tam giác vuông AHB, HE là trung tuyến ứng với cạnh huyền

\(\Rightarrow HE=\dfrac{1}{2}AB=AE\) \(\Rightarrow\Delta AHE\) cân tại E

\(\Rightarrow\widehat{AHE}=\widehat{BAH}\) (2)

Mà \(\widehat{BAH}=\widehat{MAC}\) (giả thiết) (3)

(1);(2);(3) \(\Rightarrow\widehat{AME}=\widehat{AHE}\)

\(\Rightarrow AMHE\) nội tiếp (2 góc bằng nhau cùng chắn AE)

\(\Rightarrow\) 4 điểm A, E, M, H cùng thuộc 1 đường tròn

b.

Theo cmt AMHE nội tiếp \(\Rightarrow\widehat{AEM}=\widehat{AHM}=90^0\) (cùng chắn AM)

\(\Rightarrow EM\perp AB\)

Mà \(EM||AC\)

\(\Rightarrow AB\perp AC\)

\(\Rightarrow\widehat{BAC}=90^0\)

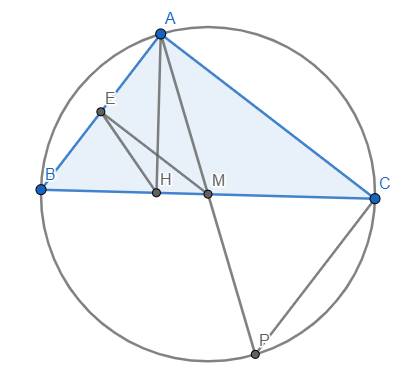
a) Gọi P là giao điểm của AM với (O). Tam giác ABH và APC có:

\(\widehat{BAH}=\widehat{PAC}\left(gt\right)\) và \(\widehat{ABH}=\widehat{APC}\) (góc nội tiếp cùng chắn cung AC)

 \(\Rightarrow\Delta ABH~\Delta APC\left(g.g\right)\) \(\Rightarrow\widehat{AHB}=\widehat{ACP}\).

 Mà \(\widehat{AHB}=90^o\Rightarrow\widehat{ACP}=90^o\) . Suy ra M nằm trên đường kính AP của (O).

 Mặt khác, M lại là trung điểm của dây BC của (O), do đó nếu dây BC không phải là đường kính của (O) thì phải có \(AP\perp BC\) , điều này không chắc chắn đúng. Do đó để đảm bảo M là trung điểm BC thì BC phải là đường kính của (O).

 \(\Rightarrow\) M là tâm của (O). Từ đó \(\widehat{MBA}=\widehat{MAB}\) 

Trong tam giác HAB vuông tại H có trung tuyến HE nên \(EH=EA=EB=\dfrac{AB}{2}\), do đó \(\widehat{ABM}=\widehat{EHB}\). 

 Từ đó suy ra \(\widehat{MAB}=\widehat{EHB}\) \(\Rightarrow\) Tứ giác AMHE nội tiếp (đpcm)

b) Từ câu a), ta có BC là đường kính của (O) nên suy ra đpcm.

Giúp em với ạ, huhu

a: Ta có: \(\widehat{MAC}=\widehat{ACB}\)

mà hai góc này là hai góc ở vị trí so le trong

nên AM//BC

Ta có: \(\widehat{NAB}=\widehat{ABC}\)

mà hai góc này là hai góc ở vị trí so le trong

nên AN//BC

Ta có: AM//BC

AN//BC

mà AM,AN có điểm chung là A

nên N,A,M thẳng hàng

b: Đặt \(\widehat{B}=x;\widehat{C}=y\)

Theo đề, ta có:

\(\left\{{}\begin{matrix}x-y=10\\x+y=110\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=60\\y=50\end{matrix}\right.\)

Bạn tự vẽ hình nha 

a) 

Xét tứ giác ACMD có :DAC=90 , DMC=90 

                                 DAC +DMC =180

nên ACMD là tứ giác nội tiếp

Xét tứ giác BCME có: CME=90 ,CBE=90

                                 CME + CBE = 180

nên BCME là tứ giác nội tiếp

b)

Theo a ta có :BCME là tứ giác nội tiếp nên MEC=MBC (cùng chắn cung MC)

                    ACMD là tứ giác nội tiếp nên MDC=MAC (cùng chắn cung MC )

a) xet 2 tg ABM va ECM ta có;

am = me (gt)

m₁ = m₂ (dđ)

mb= mc (gt)

vay 2 tg = nhau ( cgc) => c=90^o

b) ac>ec vi trong tg aec có góc e>a

c) bam>mac vi tg aec có  góc e>a  (cmt)

ma góc e = a (theo cau a)

=> góc bam>mac

Cho tam giác ABC có AC>AB,AM là trung tuyến.Trên tia đối của tia MA lấy điểm D saocho MD=MA.Nối C vs D.

a, C/m: góc ADC>DAC.Từ đó suy ra góc MAB>MAC

b, Kẻ đường cao AH.Gọi E là 1 điểm nằm giữa A và H.S²   HC và HB ;EC và EB