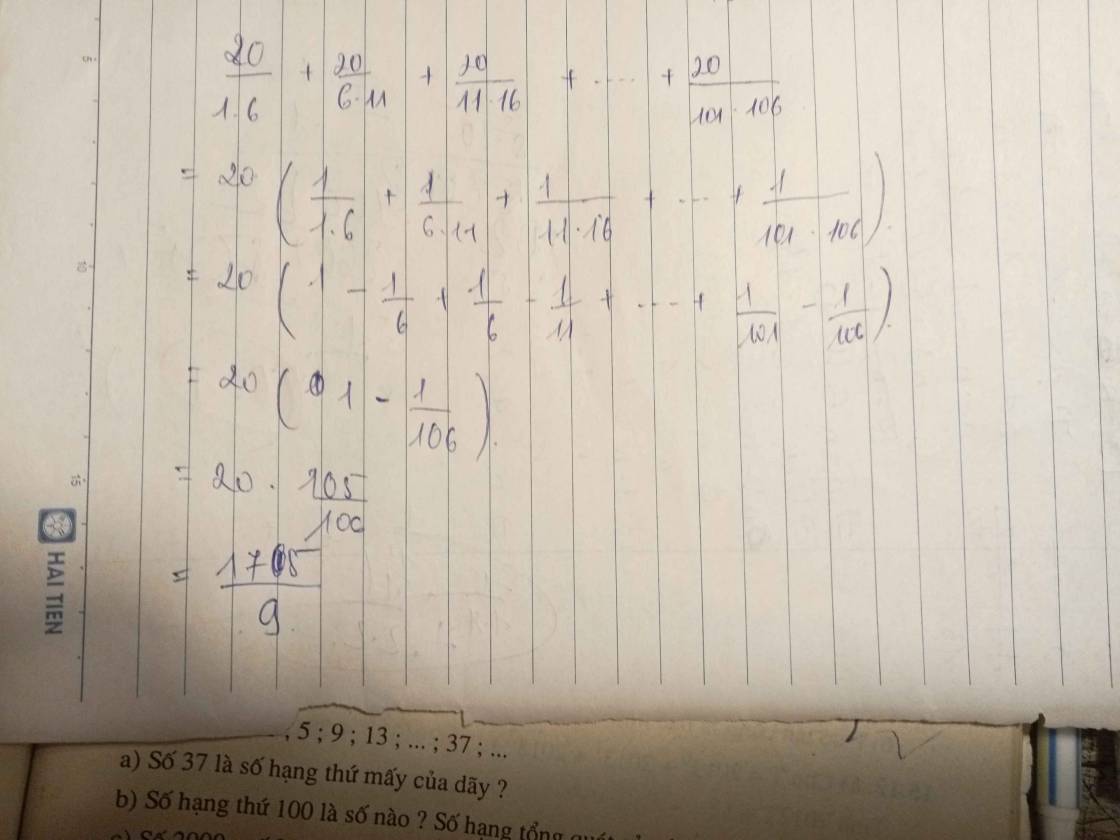\(A=\frac{20}{1\cdot6}+\frac{20}{6\cdot11}+...+\frac{20}{51\cdot56}+\frac{20}{56\cdot61}\)

\(A=\frac{20}{5}\cdot\left(1-\frac{1}{6}+\frac{1}{6}-\frac{1}{11}+...+\frac{1}{51}-\frac{1}{56}+\frac{1}{56}-\frac{1}{61}\right)\)

\(A=4\cdot\left(1-\frac{1}{61}\right)\)

\(A=4\cdot\frac{60}{61}\)

\(A=\frac{240}{61}\)

\(A=\frac{20}{1.6}+\frac{20}{6.11}+...+\frac{20}{51.56}+\frac{20}{56.61}\)

\(A=\frac{20}{5}.\left(1-\frac{1}{6}+\frac{1}{6}-\frac{1}{11}+....+\frac{1}{51}-\frac{1}{56}+\frac{1}{56}-\frac{1}{61}\right)\)

\(A=4.\left(1-\frac{1}{61}\right)\)

\(A=4.\frac{60}{61}=\frac{240}{61}\)

\(A=\dfrac{20}{1.6}+\dfrac{20}{6.11}+.........+\dfrac{20}{51.56}+\dfrac{20}{56.61}\)

\(\dfrac{1}{4}A=\dfrac{5}{1.6}+\dfrac{5}{6.11}+........+\dfrac{5}{51.56}+\dfrac{5}{56.61}\)

\(\dfrac{1}{4}A=1-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{11}+........+\dfrac{1}{51}-\dfrac{1}{56}+\dfrac{1}{56}-\dfrac{1}{61}\)

\(\dfrac{1}{4}A=1-\dfrac{1}{61}\)

\(\Rightarrow A=\dfrac{60}{61}:\dfrac{1}{4}\)

\(\Rightarrow A=\dfrac{60}{61}.4\)

\(\Rightarrow A=\dfrac{240}{61}\)

Cậu làm đúng rồi đó!!!

mình trả lời bài 1 thôi nhé :

Gọi biểu thức trên là A.

Theo bài ra ta có:A=1/1.6+1/6.11+1/11.16+...+1/(5n+1)+1/(5n+6)

                           =1/5(1-1/6+1/6-1/11+1/11-1/16+...+1/5n+1-1/5n+6)

                           =1/5(1-1/5n+6)

                           =1/5( 5n+6/5n+6-1/5n+6)

                           =1/5(5n+6-1/5n+6)

                           =1/5.5n+5/5n+6

                           =n+1/5n+6

                           =ĐIỀU PHẢI CHỨNG MINH

x- 20/11.13 - 20/13.15 - 20/13.15 - 20/15.17 -...- 20/53.55=3/11

x-10.(2/11.13+2/13.15+2/15.17+...+2/53.55=3/11

x-10.(1/11-1/13+1/13-1/15+1/15-1/17+...+1/53-1/55)=3/11

x-10.(1/11-1/55)=3/11

x-10.4/55=3/11

x-8/11=3/11

x = 3/11+8/11

x=11/11=1

****

= 1 - 1/6 + 1/6 - 1/11 + ... + 1/101 - 1/106

= 1 - 1/106

= 105/106

Ta có:\(\frac{5}{1.6}+\frac{5}{6.11}+........+\frac{5}{101.106}\)

=\(1-\frac{1}{6}+\frac{1}{6}-\frac{1}{11}+..........+\frac{1}{101}-\frac{1}{106}\)

=\(1-\frac{1}{106}\)

=\(\frac{105}{106}\)

\(=5\left(\dfrac{5}{1\cdot6}+\dfrac{5}{6\cdot11}+...+\dfrac{5}{101\cdot106}\right)\\ =5\left(1-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{11}+...+\dfrac{1}{101}-\dfrac{1}{106}\right)\\ =5\left(1-\dfrac{1}{106}\right)=5\cdot\dfrac{105}{106}=\dfrac{525}{106}\)

cảm ơn bạn

=1/5(5/1*6+5/6*11+...+5/101*106)

=1/5(1-1/6+1/6-1/11+...+1/101-1/106)

=1/5(1-1/106)

=1/5*105/106

=21/106

\(B=\dfrac{1}{1.6}+\dfrac{1}{6.11}+\dfrac{1}{11.16}+...+\dfrac{1}{101.106}\)

\(B=\dfrac{1}{5}.\left(1-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{16}+...+\dfrac{1}{101}-\dfrac{1}{106}\right)\)

\(B=\dfrac{1}{5}.\left(1-\dfrac{1}{106}\right)\)

\(B=\dfrac{1}{5}.\dfrac{105}{106}\)

\(B=\dfrac{21}{106}\)

Tính S:

S=5.(\(\dfrac{5}{1.6}\)+\(\dfrac{5}{6.11}\)+...+\(\dfrac{5}{101.106}\))

S=5.(1-\(\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{11}+...+\dfrac{1}{101}-\dfrac{1}{106}\))

S=5.(1-\(\dfrac{1}{106}\))

S=5.\(\dfrac{105}{106}\)

S=\(\dfrac{525}{106}\)

525/106