Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. có góc B cộng góc C bằng 180 độ ( tiế vậy nó nội tip tuyến ĐT) vậy nó nội tiếp
2. xét 2 tam giác ABE và tam giác AFB chứng minh nó đồng dạng (g,g), vì góc A chung, góc F bằng góc ABE = 1/2 Sđ cung BE. rồi lập tì số đồng dạng là được.
3. Chưa làm được. nếu bạn làm được rối thông tin cho mình nhé. cảm ơn

1: góc ABO+góc ACO=180 độ
=>ABOC nội tiếp đường tròn đường kính OA
Tâm là trung điểm của OA
2: Xét ΔABE và ΔAFB có
góc ABE=góc AFB
góc BAE chung
=>ΔABE đồng dạng với ΔAFB
=>AB/AF=AE/AB
=>AB^2=AE*AF

1) Ta có \(\widehat{ABO}=\widehat{ACO}=90độ\left(gt\right)\)
Do đó\(\widehat{ABO}+\widehat{ACO}=180độ\)
Nên tứ giác ABOC nội tiếp đường tròn đường kính AO
Tâm đường tròn ngoại tiếp tứ giác ABOC là trung điểm AO.
2) Xét ΔABD và ΔAEB có
\(\widehat{BAE}\)chung
\(\widehat{ABD}=\widehat{AEB}\)(góc tạo bởi tia tiếp tuyến và dây và góc nội tiếp cùng chắn \(\widebat{BD}\))
Nên ΔABD 
Do đó \(\frac{AB}{AE}\)=\(\frac{AD}{AB}\)
Hay AB2= AE.AD

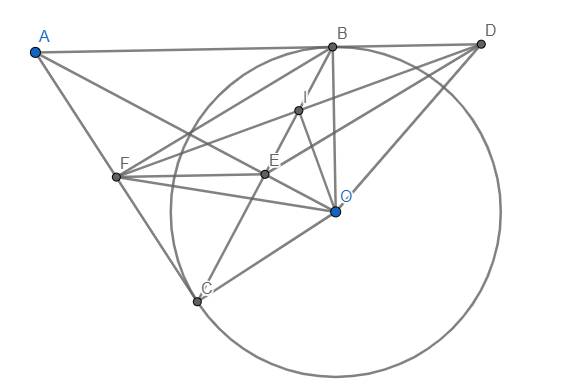
a) Nhận thấy \(\widehat{OBA}=\widehat{OCA}=90^o\) nên tứ giác ABOC nội tiếp đường tròn đường kính OA.
b) Nhân thấy \(\widehat{OID}=\widehat{OBD}=90^o\) nên tứ giác OIBD nội tiếp đường tròn đường kính OD \(\Rightarrow\widehat{IDO}=\widehat{IBO}\)
Lại có \(\widehat{IBO}=\widehat{CBO}=\widehat{BCO}\) nên dễ dàng suy ra đpcm.
c) Dễ chứng minh tứ giác OCFI nội tiếp \(\Rightarrow\widehat{OCB}=\widehat{OCI}=\widehat{OFI}=\widehat{OFD}\)
Theo câu b, ta có \(\widehat{FDO}=\widehat{IDO}=\widehat{BCO}\) nên dẫn đến \(\widehat{OFD}=\widehat{FDO}\). Do đó tam giác ODF cân tại O. (đpcm)
d) Tam giác ODF cân tại F có đường cao OI nên I là trung điểm DF.
Mặt khác, có I là trung điểm BE nên tứ giác BDEF là hình bình hành.
\(\Rightarrow\) EF//BD hay EF//AB.
Lại có E là trung điểm BC nên F là trung điểm AC (đpcm)
1. Vì BO vuông góc với BA => góc ABO = 90 độ
Vi CO vuông góc với CA => góc ACO = 90 độ
Xét tứ giác ABOC có : Góc ABC = 90 độ, Góc ACO = 90 độ
mà 2 góc trên đối nhau và có tổng = 180 độ
=> tứ giác ABOC là tứ giác nội tiếp đường tròn.
Nối A với O, ta được tam giác ABO vuông tại B.
Vẽ trung tuyến BI của tam giác ABO => IO = IA = IB
=> I là tâm đường tròn ngoại tiếp tứ giác ABOC.
2. Câu này câu hỏi là gì vậy?
3,