a: Xét ΔODK có AH//DK

nên AH/DK=OH/OK

Xét ΔOKC có HB//KC

nên HB/KC=OH/OK

=>AH/DK=HB/KC

mà AH=HB

nên DK=KC

=>K là trung điểm của CD

b: Xét ΔMAB và ΔMKD có

góc MAB=góc MKD

góc AMB=góc KMD

Do đo: ΔMAB đồng dạng với ΔMKD

=>MA/MK=AB/DK

=>MK/MA=DK/AB

Xét ΔNKC và ΔNBA có

góc NKC=góc NBA

góc KNC=góc BNA

Do đó: ΔNKC đồng dạng với ΔNBA

=>NK/NB=KC/BA=KD/AB=MK/MA

=>MN//AB

a) Dễ thấy MH là đường trung trực của AB , I thuộc MH => IN = IK

=> tam giác INK cân tại I => Góc INH = góc IKH

Mà góc MNK = góc MKN vì tam giác MNK cân tại M

=> Góc BNA = góc AKB . Dễ dàng suy ra tam giác AIN = tam giác BIK (g.c.g)

=> AN = BK . Đến đây áp dụng định lí ta lét đảo được AB // NK => ABKN là hình thang có hai góc kề 1 đáy bằng nhau => ABKN là hình thang cân

b) Dễ thấy MK là đường trung trực của NK vì tam giác MNK cân, có đường phân giác MI

Vì AB // NK nên tam giác MAB cân tại M => có điều tương tự.

Bài 2 sử dụng tính chất của hình thang cân là ra ^^

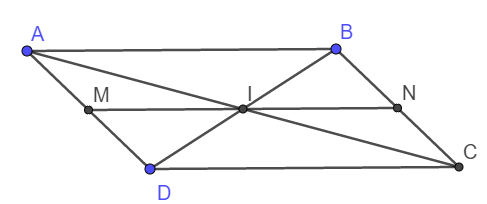
1.  Xét tam giác ABD có MI // AB nên theo định lý Talet ta có:

\(\frac{MI}{AB}=\frac{DI}{DB}\)

Xét tam giác ABC có NI // AB nên theo định lý Talet ta có:

\(\frac{NI}{AB}=\frac{NC}{BC}\)

2. Xét tam giác BDC có IN // DC nên \(\frac{DI}{DB}=\frac{NC}{BC}\)

Từ đó ta có: \(\frac{MI}{AB}=\frac{NI}{AB}\Rightarrow MI=IN\)

Vậy I là trung điểm MN (đpcm)

Khó thế ai làm được hả bạn Toàn!😢😢😢😢😢

a ) Vì \(\hept{\begin{cases}EA=ED\left(gt\right)\\FB=FC\left(gt\right)\end{cases}}\)

\(\Rightarrow\)   EF là đường trung bình của hình thang ABCD.

\(\Rightarrow\) EF // AB // CD 

Xét \(\Delta ABC\) có : \(\hept{\begin{cases}BF=FC\\FK//AB\end{cases}}\)

\(\Rightarrow AK=KC\)

Xét \(\Delta ABD\) có : \(\hept{\begin{cases}AE=ED\\EI//AB\end{cases}}\)

\(\Rightarrow BI=ID\)

Vậy \(\hept{\begin{cases}AK=KC\\BI=ID\end{cases}\left(đpcm\right)}\)

b ) Vì EF là đường trung bình của hình thang ABCD.

\(\Rightarrow EF=\frac{CD+AB}{2}=\frac{10+6}{8}=2\left(cm\right)\)

Mặt khác, ta có :   

* EI là đường trung bình của \(\Delta ABD\)

\(\Rightarrow EI=\frac{1}{2}AB=\frac{1}{2}.6=3\left(cm\right)\)

* KF là đường trung bình của  \(\Delta ABC\)

\(\Rightarrow KF=\frac{1}{2}AB=\frac{1}{2}.6=3\left(cm\right)\)

Mà : EF = EI + IK + KF

\(\Rightarrow\)   IK = EF - ( EI + KF ) = 8 - ( 3 + 3 ) = 2cm.

Vậy \(\hept{\begin{cases}EI=3cm\\KF=3cm\\IK=2cm\end{cases}}\)

Chúc bạn học tốt !!!

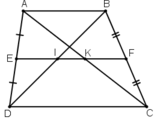
a) + Hình thang ABCD có EA = ED, FB = FC (gt)

⇒ EF là đường trung bình của hình thang ABCD.

⇒ EF // AB // CD

+ ΔABC có BF = FC (gt) và FK // AB (cmt)

⇒ AK = KC

+ ΔABD có: AE = ED (gt) và EI // AB (cmt)

⇒ BI = ID

b) + Vì EF là đường trung bình của hình thang ABCD.

⇒ EF = (AB + CD)/2 = (6 + 10)/2 = 8cm.

+ ΔABD có AE = ED, DI = IB

⇒ EI là đường trung bình của ΔABD

⇒ EI = AB/2 = 6/2 = 3(cm)

+ ΔABC có CF = BF, CK = AK

⇒ KF là đường trung bình của ΔABC

⇒ KF = AB /2 = 6/2 = 3cm

+ Lại có: EI + IK + KF = EF

⇒ IK = EF – EI – KF = 8 – 3 – 3 = 2cm