
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a, xét tam giác ABC cân tại A có AM vuông góc với BC tại M
=> tam giác ABM vuông tại M.
áp dụng đlí Pytago có: \(BM^2+AM^2=AB^2< =>AB=\sqrt{BM^2+AM^2}\)
\(=\sqrt{6^2+8^2}=10cm\)
vì tam giác ABC cân tại A=>AC=AB=10cm
b, tam giác ABC cân tại A có AM là đường cao nên đồng thời là trung tuyến=>BM=MC
xét tam giác AMB và t am giác AMC có
BM=MC(cmt) , AM chung
góc AMC= góc AMB=90 độ=>tam giác AMB=tam giác AMC(c.g.c)
c, xét tam giác ACD có AM=MD(gt)=>CM là trung tuyến
lại có CM là đường cao
=>tam giác ACD có CM vừa là đường cao vừa là trung tuyến
=>tam giác ACD cân tại C
a, dùng Pytago \(a^2+c^2=b^2\)(a,b là độ dài 2 cạnh góc vuông, b là độ dài cạnh huyền)
b, chứng minh tam giác AMB= tam giác AMC theo trường hợp cạnh góc cạnh
c, tam giác có 1 cạnh là đường cao đồng thời là trung tuyến thì tam giác đó cân

- tỉ lệ nghịch là 2 đại lượng đối nghịch nhau kiểu như cái này tăng thì cái kia giảm (tc thì xét tích tương ứng)
- tỉ lệ thuận là 2 đại lượng cùng tăng và cùng giảm (tc thì xét tỉ số)
Theo cách hiểu của t là thế
. Tỉ lệ thuận: Nếu đại lượng x tăng thì đại lượng y cũng tăng, đại lượng x giảm thì đại lượng y cũng giảm. Công thức: y = k.x (k là hằng số khác 0).
. Tỉ lệ nghịch: Nếu đại lượng x tăng lên thì đại lượng y giảm xuống, đại lượng y tăng lên thì đại lượng x giảm. Công thức: y = \(\frac{a}{x}\) hay a = x.y (a là hằng số khác 0)

a, Sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảm dần của biến là:
\(A\left(x\right)=3x^5-x^4-2x^3-2x^2+3x\)
\(B\left(x\right)=-x^5+5x^4+2x^3+2x^2-9\)
c, \(A\left(x\right)-B\left(x\right)=\left(3x^5-x^4-2x^3-2x^2+3x\right)-\left(-x^5+5x^4+2x^3+2x^2-9\right)\)
\(=3x^5-x^4-2x^3-2x^2+3x+x^5-5x^4-2x^3-2x^2+9\)
\(=\left(3x^5+x^5\right)-\left(x^4+5x^4\right)-\left(2x^3+2x^3\right)-\left(2x^2+2x^2\right)+3x+9\)
\(=4x^5-6x^4-4x^3-4x^2+3x+9\)
b,\(A\left(x\right)+B\left(x\right)=\left(3x^5-x^4-2x^3-2x^2+3x\right)+\left(-x^5+5x^4+2x^3+2x^2-9\right)\)
\(=3x^5-x^4-2x^3-2x^2+3x-x^5+5x^4+2x^3+2x^2-9\)
\(=\left(3x^5-x^5\right)+\left(-x^4+5x^4\right)+\left(-2x^3+2x^3\right)+\left(-2x^2+2x^2\right)+3x-9\)
\(=3x^5-4x^4+3x+9\)

bài này ko cần pytago cx đc:
Ta có:
CB=CD
=> FB<CD ( F nằm trên đường thẳng CB)(1)
theo đề suy ra được : tam giác EFD nằm trong tam giác EBD
<=>FD<CB ( vì FD là cạnh nằm trong tam giác và tiếp với đường cao tam giác ngoài)(2)
Từ (1) và (2) suy ra : CD+CB>FD+FB( đpcm)

\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.2^{32}}\)
Ta lấy vễ trên chia vế dưới
\(=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}\)
Ta lấy vế trên chia vế dưới
\(=2^3.3=24\)
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.3^{32}}=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}=2^3.3=8.3=24\)

Sai rồi bn ak!
Đây là cách đúng nè:
254 . 28
= (52)4 . 28
= 52 . 4 . 28
= 58 . 28
= (5 . 2)8
= 108
Sai rồi em ơi , phải như thế này cơ :
\(25^4.2^8=25^4.\left(2^2\right)^4=25^4.4^4=\left(25.4\right)^4=100^4=100000000\)





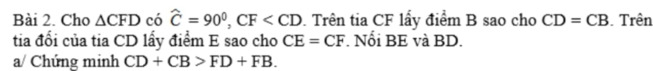
H (x) = 0
\(\Rightarrow-x^2+2x-4=0\)
\(\Rightarrow x^2-2x+4=0\)
\(\Rightarrow\left(x^2-2x+1\right)+3=0\)
\(\Rightarrow\left(x-1\right)^2+3=0\)
Mà: \(\left(x-1\right)^2+3>0\)
=> Vô lí
=> H(x) vô nghiệm
ý là mình xin công thức để áp dụng làm bài ý ạ