a: Xét ΔAOM vuông tại A có tan AOM=AM/OA=căn 3

nên góc AOM=60 độ

=>sđ cung nhỏ AI=60 độ

=>sđ cung lớn AI=300 độ

b: Xét (O) có

MA,MC là tiếp tuyến

nên MA=MC và OM là phân giác của góc COA(1)

Xét (O) có

NC,NB là tiếp tuyến

nên NC=NB và ON là phân giác của góc COB(2)

Từ (1), (2) suy ra góc MON=1/2*180=90 độ

Xét ΔMON vuông tại O có OC là đường cao

nên MC*CN=OC^2

=>AM*BN=R^2

c: góc IAC=90 độ-góc OIA

góc MAI=90 độ-góc OAI

mà góc OIA=góc OAI

nên góc IAC=góc IAM

=>AI là phân giác của góc MAC

mà MI là phân giác của góc AMC

nên I là tâm đường tròn nội tiếp ΔMAC

a: Xét (O) có

MC là tiếp tuyến

MA là tiếp tuyến

Do đó: MC=MA

Xét (O) có

DC là tiếp tuyến

DB là tiếp tuyến

Do đó: DC=DB

Ta có: CM+DC=DM

nên MD=MA+BD

a: Xét ΔMAO và ΔMCO có

MA=MC

AO=CO

MO chung

=>ΔMAO=ΔMCO

=>góc MCO=90 độ

góc MAO+góc MCO=180 độ

=>MAOC nội tiếp đường tròn đường kính MO

=>I là trung điểm của MO

b: góc MCO=90 độ

=>MC là tiếp tuyến của (O)

Xét ΔMCD và ΔMBC có

góc MCD=góc MBC

góc CMD chung

=>ΔMCD đồng dạng với ΔMBC

=>MC/MB=MD/MC

=>MC^2=MB*MD

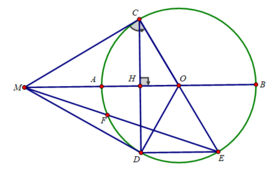
a) Xét tam giác COD cân tại O có OH là đường cao

⇒ OH cũng là tia phân giác ⇒ ∠(COM) = ∠(MOD)

Xét ΔMCO và ΔMOD có:

CO = OD

∠(COM) = ∠(MOD)

MO là cạnh chung

⇒ ΔMCO = ΔMOD (c.g.c)

⇒ ∠(MCO) = ∠(MDO)

∠(MCO) =  90 0 nên ∠(MDO) = 90 0

⇒ MD là tiếp tuyến của (O)

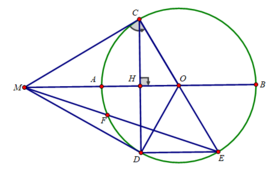
b) Ta có: OM = OA + AM = R + R = 2R

Xét tam giác MCO vuông tại C, CH là đường cao có:

MO 2 = MC 2 + OC 2

CH.OM = CM.CO

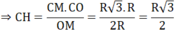
Lại có: CD = 2CH ⇒ CD = R 3

Tam giác CDE nội tiếp (O) có CE là đường kính nên ΔCDE vuông tại D

Theo định lí Py ta go ta có:

CE 2 = CD 2 + DE 2

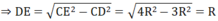
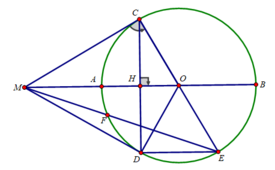
d) Ta có: ∠(CFE) = 90 0  (F thuộc đường tròn đường kính CE)

Lại có CF là đường cao nên MC 2  = MF.ME

Tương tự, ta có:  MC 2  = MH.MO

⇒ ME.MF = MH.MO

⇒

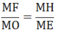
Xét ΔMOF và ΔMEN có:

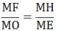
∠(FMO) chung

⇒ ΔMOF ∼ ΔMEN (c.g.c)

⇒ ∠(MOF) = ∠(MEH)

a.

Do AM là tiếp tuyến của (O) \(\Rightarrow AM\perp OA\Rightarrow\widehat{OAM}=90^0\)

\(\Rightarrow\) 3 điểm O, A, M cùng thuộc đường tròn đường kính OM (1)

Tương tự, do MC là tiếp tuyến của (O) \(\Rightarrow\widehat{OCM}=90^0\)

\(\Rightarrow\) 3 điểm O, C, M cùng thuộc đường tròn đường kính OM (2)

(1);(2) \(\Rightarrow\) 4 điểm O, A, M, C cùng thuộc đường tròn đường kính OM

b.

Do M là giao điểm 2 tiếp tuyến của (O) tại A và C \(\Rightarrow MA=MC\) (t/c hai tiếp tuyến cắt nhau)

Lại có \(OA=OC=R\)

\(\Rightarrow OM\)  là trung trực của AC

\(\Rightarrow OM\perp AC\) tại I

c.

Do AB là đường kính và D thuộc đường tròn \(\Rightarrow\widehat{ADB}\) là góc nội tiếp chắn nửa đường tròn

\(\Rightarrow\widehat{ADB}=90^0\) hay \(AD\perp BM\)

Áp dụng hệ thức lượng trong tam giác vuông BAM với đường cao AD:

\(AM^2=MD.MB\) (3)

Theo c/m câu b ta có \(AI\perp MO\), áp dụng hệ thức lượng trong tam giác vuông OAM với đường cao AI:

\(AM^2=MI.MO\) (4)

(3);(4) \(\Rightarrow MA^2=MI.MO=MD.MB\)

d.

Áp dụng hệ thức lượng trong tam giác vuông OAM với đường cao AI:

\(OA^2=OI.OM\)

Mà \(OA=OB=R\Rightarrow OB^2=OI.OM\Rightarrow\dfrac{OI}{OB}=\dfrac{OB}{OM}\)

Xét hai tam giác BOI và MOB có:

\(\left\{{}\begin{matrix}\dfrac{OI}{OB}=\dfrac{OB}{OM}\left(cmt\right)\\\widehat{MOB}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta BOI\sim\Delta MOB\left(c.g.c\right)\)

\(\Rightarrow\widehat{OIB}=\widehat{OBM}\)