Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tam giác ABC vuông ở A cho ta góc BAC =90 độ
MD vuông góc với AB => góc MDA =90 độ
ME vuông góc với AC => góc MEA =90 độ
=> tứ giác ADME là hình chữ nhật => DE=AM =>DE min<=> AM min <=> AM vuông góc với BC
Vậy M là chân đường cao kẻ từ A , M thuộc BC thì DE có độ dài nhỏ nhất

a) Chứng minh H A B ^ = E A B ^ ; H A C ^ = F A C ^ ⇒ E A F ^ = 180 0
B) Chứng minh: E B C ^ + F C B ^ = 2 ( A B C ^ + A C B ^ )
= 1800 Þ EB//FC.
Hay EBCF là hình thang. Nếu EBCF là hình thang vuông thì AH vuông BC. Nếu EBCF là hình bình hành thì H là trung điểm BC.
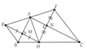
Hình vẽ:
Lời giải:
Lấy $K, H$ lần lượt đối xứng với $M$ qua $AB,AC$.
Theo tính chất đối xứng: $EK=EM; FM=FH$
Chu vi tam giác $MEF$:
$ME+EF+MF=EK+FH+EF\geq KH(*)$
Vì $M$ cố định và tam giác $ABC$ cố định nên $KH$ cố định
Vậy chu vi $MEF$ nhỏ nhất bằng $KH$. Điều này xảy ra khi $E,F$ là giao điểm của $KH$ với lần lượt $AB,AC$