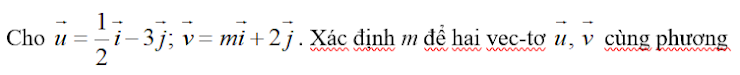thi ko giúp nhoa

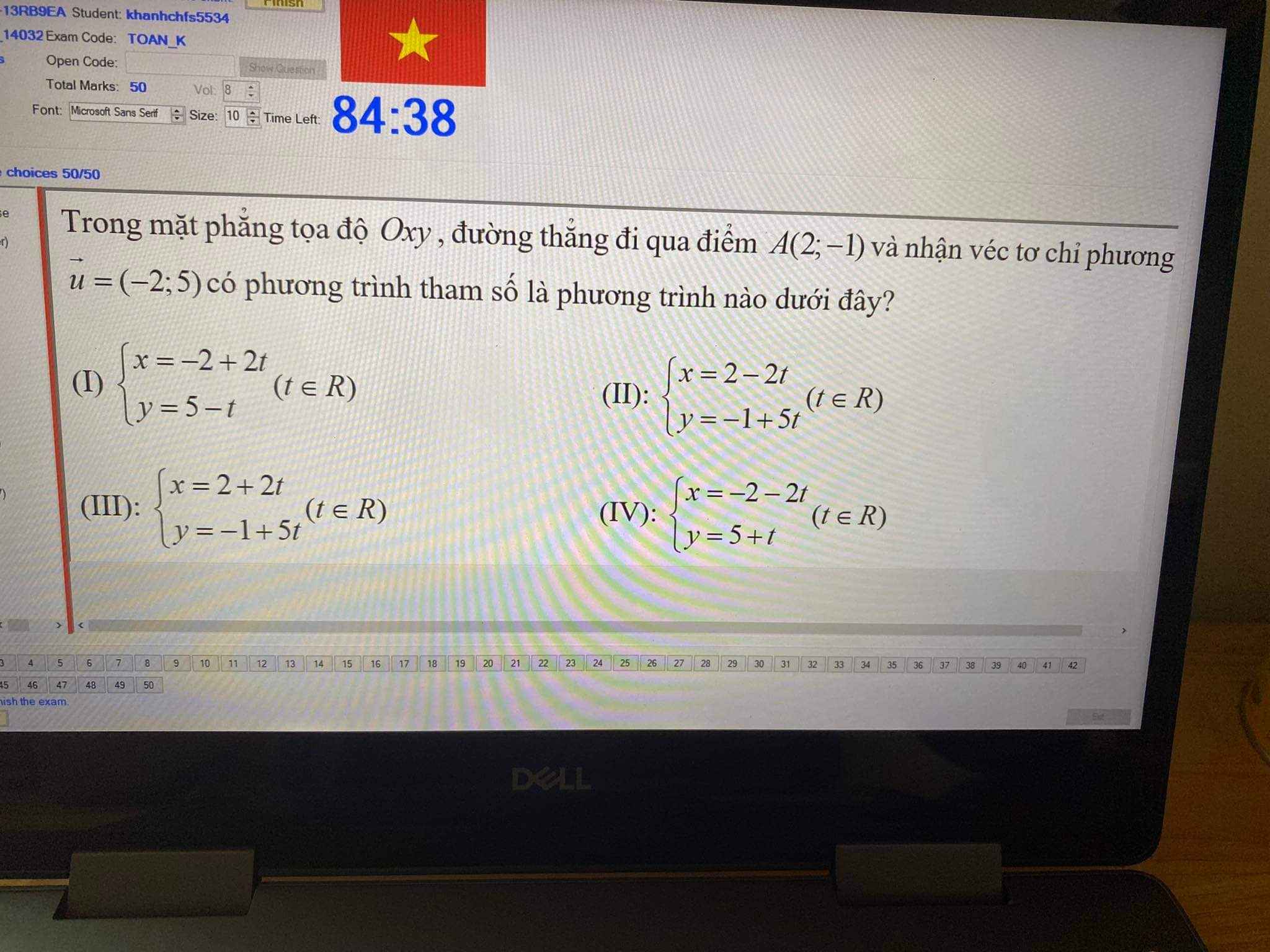
Chọn ý (II).

\(\left\{{}\begin{matrix}x=2-2t\\y=-1+5t\end{matrix}\right.\left(t\in R\right)\).

\(VD5\)

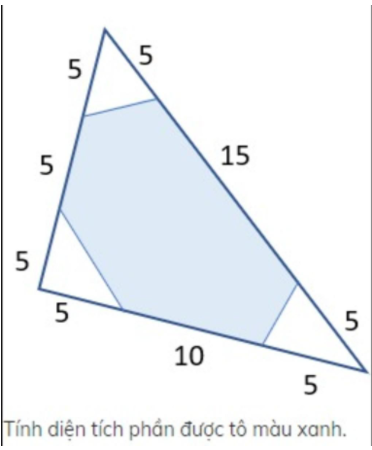
\(\overrightarrow{AB}=\left(2;6\right)\\ =>AB=\sqrt{2^2+6^2}=2\sqrt{10}\\ \overrightarrow{AC}=\left(15;5\right)\\=>AC=\sqrt{15^2+5^2}=5\sqrt{10}\)

Giả sử \(AD\) là tia phân giác của góc \(A\)

\(\Rightarrow\dfrac{BD}{DC}=\dfrac{AB}{AC}=\dfrac{2\sqrt{10}}{5\sqrt{10}}=\dfrac{2}{5}\)

mà \(\overrightarrow{BD},\overrightarrow{DC}\) cùng phương

\(\Rightarrow\overrightarrow{BD}=\dfrac{2}{5}\overrightarrow{DC}\)

Giả sử điểm \(D(x;y)\)

\(=>\overrightarrow{BD}=\left(x+4;y-3\right)\\ \dfrac{2}{3}\overrightarrow{DC}=\dfrac{2}{3}.\left(9-x;2-y\right)=\left(6-9x;\dfrac{4}{3}-\dfrac{2}{3}y\right)\)

\(\Rightarrow\left\{{}\begin{matrix}x+4=6-9x\\y-3=\dfrac{4}{3}-\dfrac{2}{3}y\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x=\dfrac{1}{5}\\y=\dfrac{13}{5}\end{matrix}\right.\\ =>D\left(\dfrac{1}{5};\dfrac{13}{5}\right)\)

\(\Rightarrow\overrightarrow{AD}=\left(\dfrac{31}{5};\dfrac{28}{5}\right)\) là vt chỉ phương

\(\Rightarrow\overrightarrow{n}=\left(-\dfrac{28}{5};\dfrac{31}{5}\right)\) là vt pháp tuyến

Đường thẳng \(AD\) đi qua \(A\left(-6;-3\right)\) và nhận \(\overrightarrow{n}\) là vt pháp tuyến có pt

\(-\dfrac{28}{5}\left(x+6\right)+\dfrac{31}{5}\left(y+3\right)=0\\ =>-\dfrac{28}{5}x+\dfrac{31}{5}y-15=0\)

bạn ơi bạn có nhầm ko chứ  \(\overrightarrow{BD}\) = \(\dfrac{3}{5}\)\(\overrightarrow{DC}\)    _{^{mà sau khi biến đổi sang tọa độ bạn lại dùng \(\dfrac{2}{3}\)}}

\(\Leftrightarrow m:\dfrac{1}{2}=\dfrac{-3}{2}\)

hay m=-3/4

DĐáp án chỉ có những đáp án này thôi ạ:

m = 3
m = - 1/3
m = - 2
m = 1/2

27B

28C

29D

30B

31A

32C

33C

34A

TH1: 1,2 đứng đầu

=>Có \(2\cdot2\cdot4=16\left(cách\right)\)

TH2: 1,2 đứng giữa

Nếu số 0 đứng cuối thì có \(2\cdot1\cdot4=8\left(cách\right)\)

Nếu số 8 đứng cuối thì có \(2\cdot1\cdot3=6\left(cách\right)\)

=>Có 14 cách

TH3: 1,2 đứng cuối

=>Có \(1\cdot4\cdot3=12\left(cách\right)\)

=>Có 16+14+12=42 cách