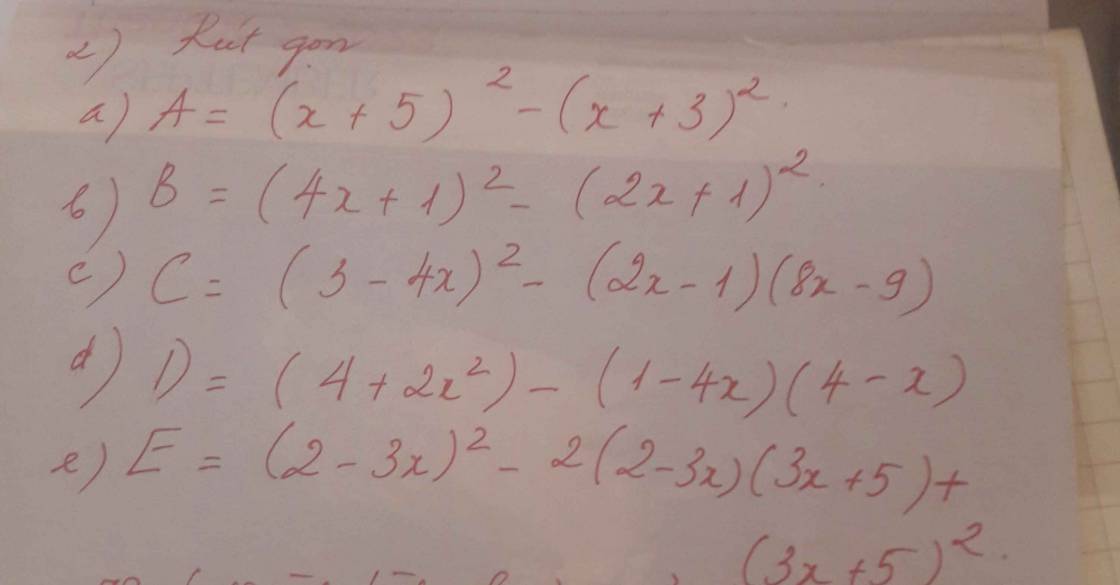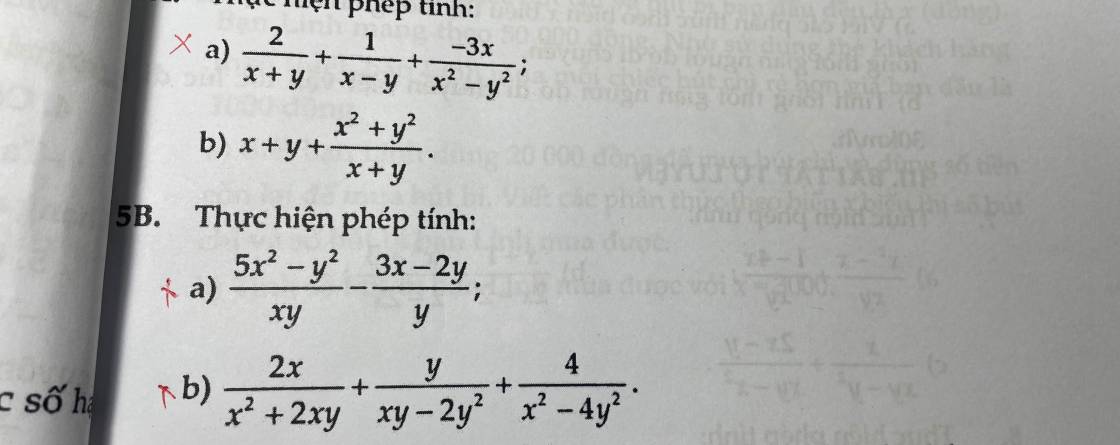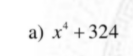a) \(A=\left(x+5\right)^2-\left(x+3\right)^2\)

\(=\left[\left(x+5\right)-\left(x+3\right)\right]\left[\left(x+5\right)+\left(x+3\right)\right]\)

\(=\left(x+5-x-3\right)\left(x+5+x+3\right)\)

\(=2\left(2x+8\right)\)

\(=4x+16\)

b) \(B=\left(4x+1\right)^2-\left(2x+1\right)^2\)

\(=\left[\left(4x+1\right)-\left(2x+1\right)\right]\left[\left(4x+1\right)+\left(2x+1\right)\right]\)

\(=\left(4x+1-2x-1\right)\left(4x+1+2x+1\right)\)

\(=2x\left(6x+2\right)\)

\(=12x^2+4x\)

c) \(C=\left(3-4x\right)^2-\left(2x-1\right)\left(8x-9\right)\)

\(=9-24x+16x^2-16x^2+18x+8x-9\)

\(=\left(16x^2-16x^2\right)+\left(-24x+18x+8x\right)+\left(9-9\right)\)

\(=2x\)

d) \(D=\left(4+2x^2\right)-\left(1-4x\right)\left(4-x\right)\)

\(=4+2x^2-4+x+16x-4x^2\)

\(=\left(2x^2-4x^2\right)+\left(x+16x\right)+\left(4-4\right)\)

\(=-2x^2+17x\)

e) \(E=\left(2-3x\right)^2-2\left(2-3x\right)\left(3x+5\right)+\left(3x+5\right)^2\)

\(=\left(2-3x+3x+5\right)^2\)

\(=7^2\)

\(=49\)

1. a

$(3x+5)^2=(3x)^2+2.3x.5+5^2$

$=9x^2+30x+25$

1.b 

$(6x^2+\frac{1}{3})^2=(6x^2)^2+2.6x^2.\frac{1}{3}+(\frac{1}{3})^2$

$=36x^4+4x^2+\frac{1}{9}$

1.c

$(5x-4y)^2=(5x)^2-2.5x.4y+(4y)^2$

$=25x^2-40xy+16y^2$

1.d

(2x^2y-3y^3x)^2=(2x^2y)^2-2.2x^2y.3y^3x+(3y^3x)^2$

$=4x^4y^2-12x^3y^4+9x^2y^6$

1.e

$(5x-3)(5x+3)=(5x)^2-3^2=25x^2-9$

1.f

$(6x+5y)(6x-5y)=(6x)^2-(5y)^2=36x^2-25y^2$

1.g

$(-4xy-5)(5-4xy)=(-4xy-5)(-4xy+5)$

$=(-4xy)^2-5^2=16x^2y^2-25$

1.h

$(a^2b+ab^2)(ab^2-a^2b)=(ab^2+a^2b)(ab^2-a^2b)$

$=(ab^2)^2-(a^2b)^2=a^2b^4-a^4b^2$

Ta có: \(7x+4=x-2m\left(1\right)\)

Thay \(x=6\) vào \(\left(1\right)\) ta có:

\(7.6+4=6-2m\)

\(\Rightarrow46=6-2m\)

\(\Rightarrow-2m=40\)

\(\Rightarrow m=-20\)

5:

a: AD/CD=BA/BC=3/5

b: ΔBAD đồng dạng vói ΔBHD

ΔCHD đồng dạng với ΔCAB

c: ΔCHD đồng dạng với ΔCAB

=>HD/AB=CD/CB

=>HD*CB=AB*CD

a1/\(\dfrac{2}{x+y}+\dfrac{1}{x-y}+\dfrac{-3x}{x^2-y^2}\)
\(=\dfrac{2\left(x-y\right)}{\left(x+y\right)\left(x-y\right)}+\dfrac{x+y}{\left(x+y\right)\left(x-y\right)}+\dfrac{-3x}{\left(x+y\right)\left(x-y\right)}\)
\(=\dfrac{2x-2y+x+y-3x}{\left(x+y\right)\left(x-y\right)}\)
\(=\dfrac{-y}{\left(x+y\right)\left(x-y\right)}\)
a2/\(\dfrac{5x^2-y^2}{xy}-\dfrac{3x-2y}{y}\)
\(=\dfrac{5x^2-y^2}{xy}-\dfrac{3x^2-2xy}{xy}\)
\(=\dfrac{5x^2-y^2-3x^2+2xy}{xy}\)
\(=\dfrac{2x^2-y^2+2xy}{xy}\)
b/\(\dfrac{2x}{x^2+2xy}+\dfrac{y}{xy-2y^2}+\dfrac{4}{x^2-4y^2}\)
\(=\dfrac{2x}{x\left(x+2y\right)}+\dfrac{y}{y\left(x-2y\right)}+\dfrac{4}{\left(x-2y\right)\left(x+2y\right)}\)
\(=\dfrac{2}{x+2y}+\dfrac{1}{x-2y}+\dfrac{4}{\left(x-2y\right)\left(x+2y\right)}\)
\(=\dfrac{2\left(x-2y\right)}{\left(x-2y\right)\left(x+2y\right)}+\dfrac{x+2y}{\left(x-2y\right)\left(x+2y\right)}+\dfrac{4}{\left(x-2y\right)\left(x+2y\right)}\)
\(=\dfrac{2x-4y+x+2y+4}{\left(x-2y\right)\left(x+2y\right)}\)
\(=\dfrac{3x-2y+4}{\left(x-2y\right)\left(x+2y\right)}\)
#TienDatzZz

a) \(\dfrac{2}{x+y}+\dfrac{1}{x-y}+\dfrac{-3x}{x^2-Y^2}\)

\(\dfrac{2\left(x-y\right)}{\left(x+y\right)\left(x-y\right)}+\dfrac{\left(x+y\right)}{\left(x+y\right)\left(x-y\right)}+\dfrac{-3x}{x^2-y^2}\)

\(\dfrac{2x-2y+x+y-3x}{x^2-y^2}\)

\(\dfrac{-y}{x^2-y^2}\)

\(\left(n-1\right)^2\left(n+1\right)+\left(n-1\right)\left(n+1\right)\)

\(=\left(n-1\right)\left(n+1\right)\left[\left(n-1\right)+1\right]\)

\(=\left(n-1\right)\left(n+1\right)\left(n-1+1\right)\)

\(=n\left(n-1\right)\left(n+1\right)\)

Xét: 

\(n\left(n-1\right)\) là hai số tự nhiên liên tiếp nên sẽ có số chẵn nên sẽ chia hết cho 2

\(n\left(n-1\right)\left(n+1\right)\) là 3 số tự nhiên liên tiếp nên sẽ chia hết cho 3

Mà: (2;3)=1 nên

\(n\left(n-1\right)\left(n+1\right)\) sẽ chia hết cho 2 x 3 =  6 (đpcm)

\(\left(n-1\right)^2\left(n+1\right)+\left(n-1\right)\left(n+1\right)\)

\(=\left(n-1\right)\left(n+1\right)\left(n-1+1\right)\)

\(=\left(n-1\right)n\left(n+1\right)\) là 3 số tự nhiên liên tiếp

\(\Rightarrow\left\{{}\begin{matrix}\left(n-1\right)n\left(n+1\right)⋮2\\\left(n-1\right)n\left(n+1\right)⋮3\end{matrix}\right.\)

\(\Rightarrow\left(n-1\right)n\left(n+1\right)⋮\left(2.3\right)\)

mà \(UCLN\left(2;3\right)=1\)

\(\Rightarrow\left(n-1\right)n\left(n+1\right)⋮6\)

\(\Rightarrow dpcm\)

\(x^4+324=\left(x^4+36x^2+324\right)-36x^2\)

\(=\left(x^2+18\right)^2-36x^2\)

\(=\left(x^2-6x+18\right)\left(x^2+6x+18\right)\)

Đây là dùng CT thêm và bớt phải ko cậu