
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




a: Ta có: \(AN=NB=\dfrac{AB}{2}\)
\(AM=MC=\dfrac{AC}{2}\)
mà AB=AC
nên AN=NB=AM=MC
Xét ΔNBC và ΔMCB có
NB=MC
\(\widehat{NBC}=\widehat{MCB}\)(ΔABC cân tại A)
BC chung
Do đó: ΔNBC=ΔMCB
b: Xét ΔABC có
AD,BM,CN là các đường trung tuyến
AD,BM,CN đồng quy tại G
Do đó: G là trọng tâm của ΔABC
=>\(AG=2GD\)
mà AG=GE
nên GE=2GD
=>D là trung điểm của GE
=>DG=DE
c: Ta có: ΔABC cân tại A
mà AD là đường trung tuyến
nên AD\(\perp\)BC
Xét ΔCGE có
CD là đường cao
CD là đường trung tuyến
Do đó: ΔCGE cân tại C
d: Xét ΔABC có
BM là đường trung tuyến
G là trọng tâm
Do đó: \(BG=\dfrac{2}{3}BM=10\left(cm\right)\)
D là trung điểm của BC
=>DB=DC=BC/2=8(cm)
ΔGDB vuông tại D
=>\(GD^2+DB^2=GB^2\)
=>\(GD^2=10^2-8^2=36\)
=>\(GD=\sqrt{36}=6\left(cm\right)\)
\(\Leftrightarrow AG=2\cdot GD=12\left(cm\right)\)


Do \(\overline{2x9y1}\) là số chính phương \(\Rightarrow\overline{2x9y1}=k^2\)
\(\overline{2x9y1}\) có tận cùng bằng 1 \(\Rightarrow k\) tận cùng bằng 1 hoặc 9
Mặt khác \(20164< \overline{2x9y1}< 30276\Rightarrow142^2< \overline{2x9y1}< 174^2\)
\(\Rightarrow142^2< k^2< 174^2\)
\(\Rightarrow142< k< 174\)
Do k có tận cùng bằng 1 hoặc 9 \(\Rightarrow\) k chỉ có thể là 1 trong các số: 149, 151, 159, 161, 169, 171
Kiểm tra ta thấy chỉ có \(k=161\Rightarrow k^2=25921\) là có dạng thỏa mãn \(\overline{2x9y1}\)
Vậy \(\left\{{}\begin{matrix}x=5\\y=2\end{matrix}\right.\)

Đề bài thiếu bạn nhé, có lẽ là x và y là các số nguyên.



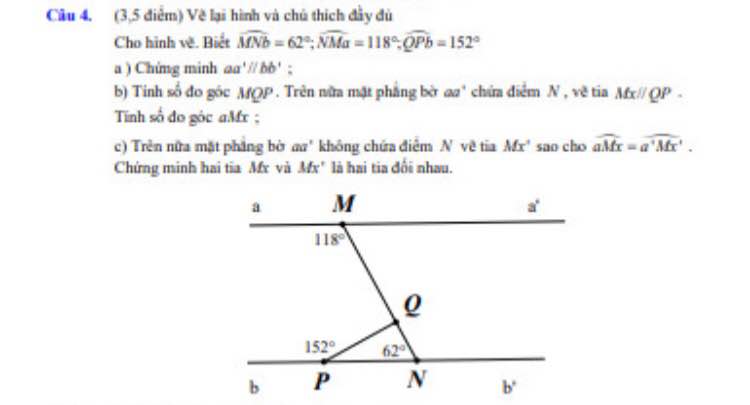
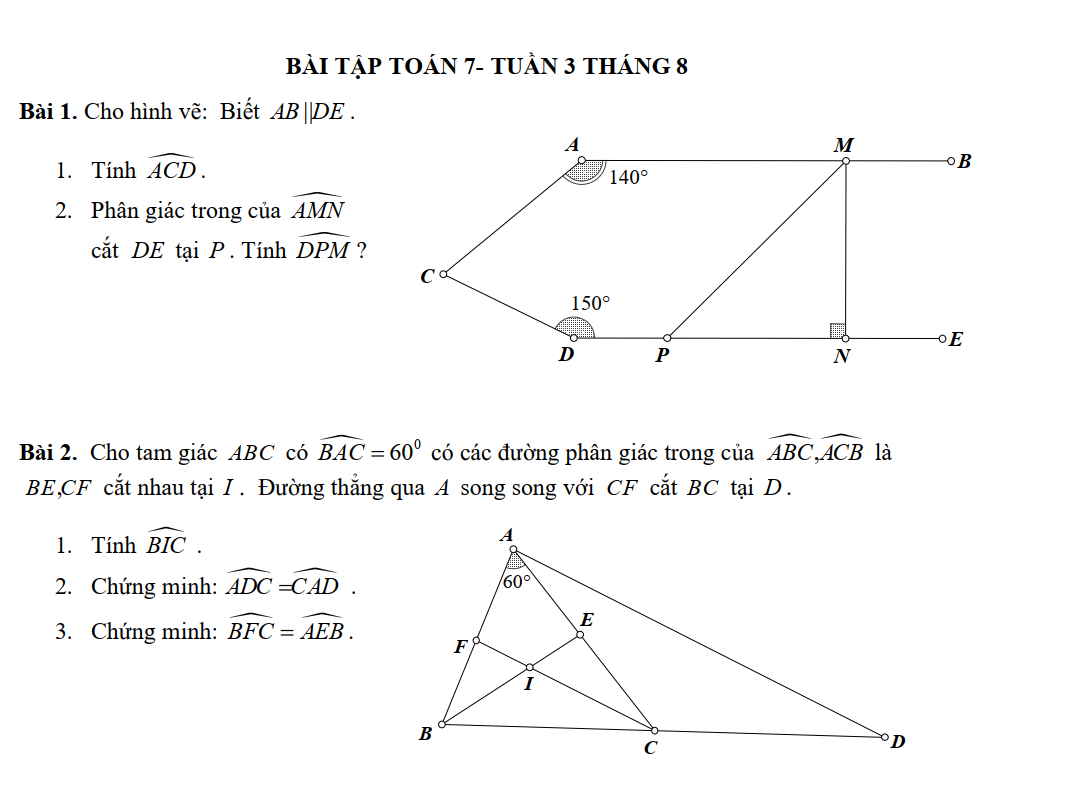
Bài 1:
1) Kẻ tia Cx//AB//DE
Ta có: Cx//AB
\(\Rightarrow\widehat{BAC}+\widehat{ACx}=180^0\)(2 góc trong cùng phía)
\(\Rightarrow\widehat{ACx}=180^0-\widehat{BAC}=180^0-140^0=40^0\)
Ta có: Cx//DE
\(\Rightarrow\widehat{xCD}+\widehat{CDE}=180^0\)( 2 góc trong cùng phía)
\(\Rightarrow\widehat{xCD}=180^0-\widehat{CDE}=180^0-150^0=30^0\)
\(\Rightarrow\widehat{ACD}=\widehat{ACx}+\widehat{xCD}=40^0+30^0=70^0\)
2) Ta có AB//DE(gt)
Mà DE⊥MN
=> AB⊥MN =>\(\widehat{AMN}=90^0\Rightarrow\dfrac{1}{2}\widehat{AMN}=45^0\Rightarrow\widehat{AMP}=45^0\) (do MP là tia phân giác \(\widehat{AMN}\))
Ta có AB//DE
=> \(\widehat{AMP}+\widehat{DPM}=180^0\) (2 góc trong cùng phía)
\(\Rightarrow\widehat{DPM}=180^0-\widehat{AMP}=180^0-45^0=135^0\)
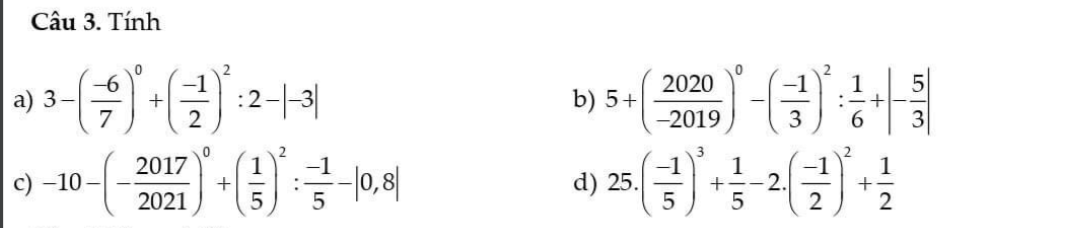




c: \(-10-\left(\dfrac{-2017}{2021}\right)^0+\left(\dfrac{1}{5}\right)^2:\dfrac{-1}{5}-\left|0.8\right|\)
\(=-11+\dfrac{1}{5^2}\cdot\dfrac{-5}{1}-\dfrac{4}{5}\)
\(=-11+\dfrac{-1}{5}-\dfrac{4}{5}\)
=-11-1
=-12