
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(x=\sqrt{27+10\sqrt{2}}-\sqrt{18+8\sqrt{2}}+8\)
\(=\sqrt{\left(5+\sqrt{2}\right)^2}-\sqrt{\left(4+\sqrt{2}\right)^2}+8\)
\(=5+\sqrt{2}-4-\sqrt{2}+8=9\)
Khi x=9 thì \(A=\dfrac{3-1}{3-2}=\dfrac{2}{1}=2\)
b: \(P=B:A\)
\(=\dfrac{x-\sqrt{x}+2}{x-\sqrt{x}-2}:\dfrac{\sqrt{x}-1}{\sqrt{x}-2}\)
\(=\dfrac{x-\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}-2}{\sqrt{x}-1}\)
\(=\dfrac{x-\sqrt{x}+1}{x-1}\)
c: \(P\cdot\sqrt{x}>=-\dfrac{3}{2}\)
=>\(\dfrac{x\sqrt{x}-x+\sqrt{x}}{x-1}+\dfrac{3}{2}>=0\)
=>\(\dfrac{2x\sqrt{x}-2x+2\sqrt{x}+3x-3}{2\left(x-1\right)}>=0\)
=>\(\dfrac{2x\sqrt{x}+x+2\sqrt{x}-1}{2\left(x-1\right)}>=0\)
TH1: \(\left\{{}\begin{matrix}2x\sqrt{x}+x+2\sqrt{x}-1>=0\\x-1>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>1\\x>=0,38\end{matrix}\right.\)
=>x>1
=>\(x\in N\backslash\left\{0;1;4\right\}\)
TH2: \(\left\{{}\begin{matrix}2x\sqrt{x}+x+2\sqrt{x}-1< =0\\x-1< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< 1\\x< =0,38\end{matrix}\right.\)
=>0<=x<0,38
mà x nguyên
nên \(x=0\)


a: góc AEB=góc AHB=90 độ
=>ABHE nôi tiếp
b: Gọi N là trung điểm của AB
=>AN=HN=EN=BN
MN là đường trung bình của ΔABC
=>MN//AC
HE vuông góc AC
=>HE vuông góc MN
=>MN là trung trực của HE
=>ME=MH

Tự vẽ hình
Kẻ BH \(\perp\)AC và \(CK\perp\)AB
Tam giác AKC vuông tại K
=>CK=bsinA (1)
Tam giác BKC vuông tại K
=>CK=asinB (2)
Từ (1) (2)=>bsinA=asinB
<=>\(\frac{a}{sinA}=\frac{b}{sinB}\)
Chứng minh tương tự ta có :\(\frac{a}{sinA}=\frac{c}{sinC}\)
Vậy ....

a) Kẻ đường cao : BH , AI , CK
Ta có: sinA = BH / c ; sinB = AI / c
=> sinA/sinB = BH / AI (1)
Mà BH = a.sinC ; AI = b.sinC
=> BH/AI = a/b (2)
Từ (1) và (2)
=> sinA/sinB = a/b => a/sinA = b/sinB
CMTT ta có:
b/sinB = c/sinC ; c/sinC = a/sinA
Từ đó suy ra a /sinA = b / sinB = c /sinC

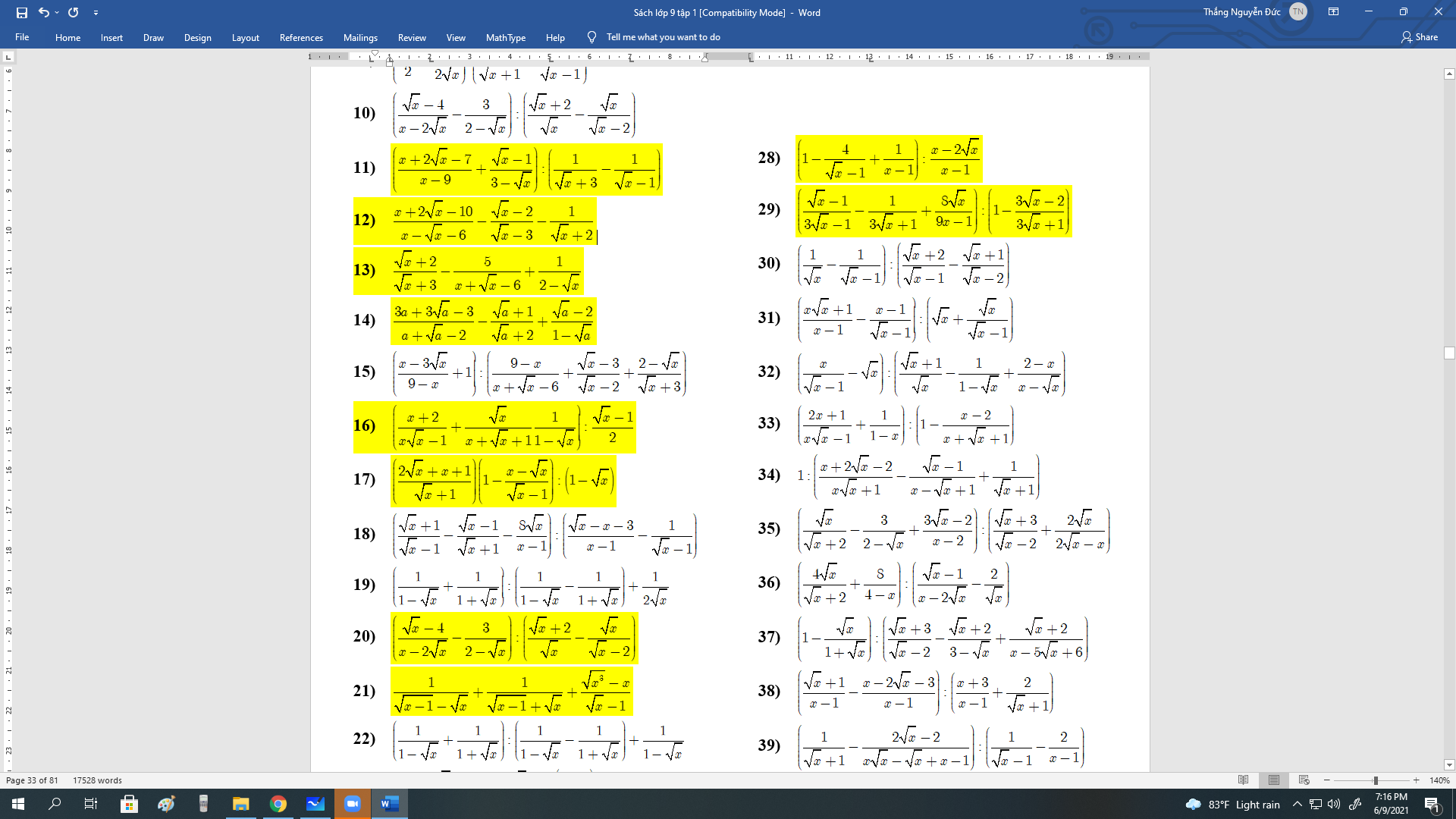
10: Ta có: \(\left(\dfrac{x-4}{x-2\sqrt{x}}+\dfrac{3}{\sqrt{x}-2}\right):\left(\dfrac{\sqrt{x}+2}{\sqrt{x}}-\dfrac{\sqrt{x}}{\sqrt{x}-2}\right)\)
\(=\dfrac{x+3\sqrt{x}-4}{\sqrt{x}\left(\sqrt{x}-2\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{x-4-x}\)
\(=\dfrac{-x-3\sqrt{x}+4}{4}\)

3: P=A*B
\(=\dfrac{2\sqrt{x}+5}{\sqrt{x}-1}\cdot\dfrac{\sqrt{x}-1}{\sqrt{x}+3}\)
\(=\dfrac{2\sqrt{x}+5}{\sqrt{x}+3}\)
\(P-1=\dfrac{2\sqrt{x}+5-\sqrt{x}-3}{\sqrt{x}+3}=\dfrac{\sqrt{x}+2}{\sqrt{x}+3}>0\)
=>P>1
=>\(P>\sqrt{P}\)

a: Áp dụng định lí Pytago vào ΔADC vuông tại D, ta được:
\(AC^2=AD^2+DC^2\)
\(\Leftrightarrow AC^2=8^2+15^2=289\)
hay AC=17cm
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔADC vuông tại D có DM là đường cao ứng với cạnh huyền AC, ta được:
\(DM\cdot AC=AD\cdot DC\)
\(\Leftrightarrow DM=\dfrac{120}{17}\left(cm\right)\)
a ) Theo định lý py-ta-go trong ΔADC, ta có :
AC^2 = AD^2 + CD^2
= 8^2 + 15^2
= 64 + 225
= 289
=> AC = 17 (cm)
b ) Ta có :
Xét tam giác ΔMDA và ΔDCA, có :
góc A chung
góc AMD = góc ADC = 90 độ
=> ΔMDA ∼ ΔDCA (G.G)
=> MD/CD = AD/AC
=> MD = CD.AD/AC
= 15.8/17
= 7,1 (cm)
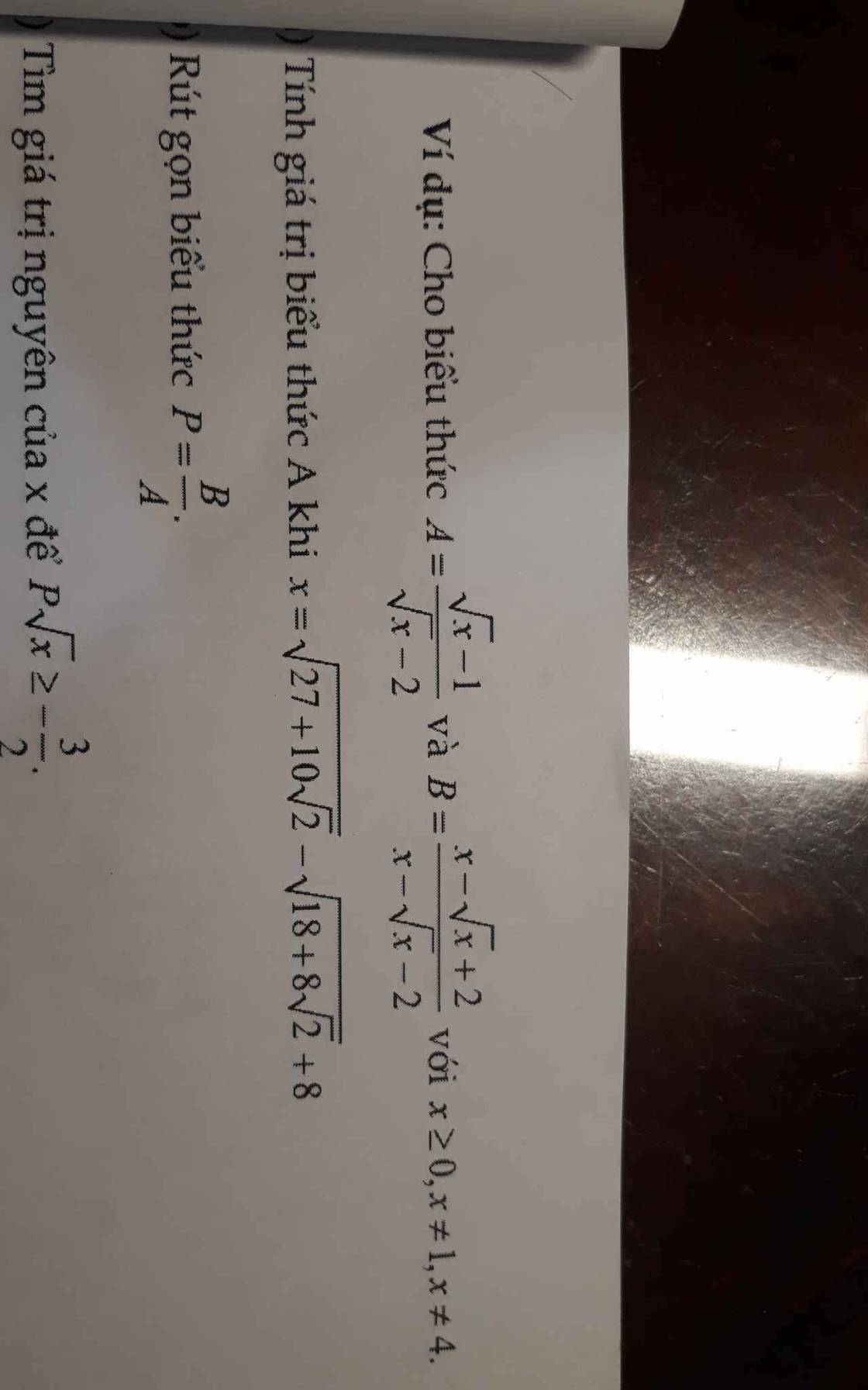 Giúp mình ý c với
Giúp mình ý c với

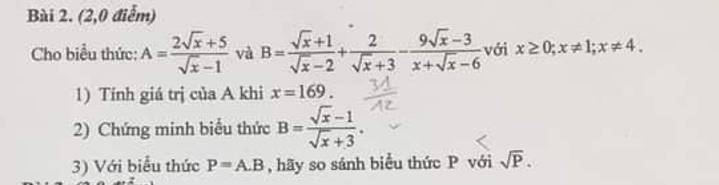

b: \(\sqrt{9-4\sqrt{2}}=2\sqrt{2}-1\)
c: \(\sqrt{9+4\sqrt{2}}=2\sqrt{2}+1\)