Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:
A H 2 = H B . H C
Suy ra:


Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AH^2=HB\cdot HC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=40cm\\AC=8\sqrt{89}cm\end{matrix}\right.\)
Xét ΔACH vuông tại H có
\(\sin\widehat{C}=\dfrac{AH}{AC}=\dfrac{5}{\sqrt{89}}\)
\(\Leftrightarrow\widehat{C}\simeq32^0\)
hay \(\widehat{B}=58^0\)

Tam giác ABC vuông ở A, ta có:
AH2 = 25.64 = 1600, suy ra AH = 40 (cm).
\(tgB=\frac{AH}{BH}=\frac{40}{25}=1,6\)
=> \(\widehat{B}\approx58^0\); \(\widehat{C}=32^0\).
hình đây nha
Ta có : AH^2 = CH . HB
=>AH=40
Ta lại có:tan B = AH / HB=40/25=1.6
=>B = 580
=>C = 320

Lời giải:
$BC=BH+CH=25+64=89$ (cm)
Áp dụng công thức hệ thức lượng trong tam giác vuông:
$AH^2=BH.CH=25.64\Rightarrow AH=40$ (cm)
Diện tích tam giác $ABC$ là: $AH.BC:2=40.89:2=1780$ (cm2)

a) \(AH^2=HB.HC=50.8=400\)
\(\Rightarrow AH=20\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.20\left(50+8\right)=\dfrac{1}{2}.20.58\left(cm^2\right)\)
mà \(S_{ABC}=\dfrac{1}{2}AB.AC\)
\(\Rightarrow AB.AC=20.58=1160\)
Theo Pitago cho tam giác vuông ABC :
\(AB^2+AC^2=BC^2\)
\(\Rightarrow\left(AB+AC\right)^2-2AB.AC=BC^2\)
\(\Rightarrow\left(AB+AC\right)^2=BC^2+2AB.AC\)
\(\Rightarrow\left(AB+AC\right)^2=58^2+2.1160=5684\)
\(\Rightarrow AB+AC=\sqrt[]{5684}=2\sqrt[]{1421}\left(cm\right)\)
Chu vi Δ ABC :
\(AB+AC+BC=2\sqrt[]{1421}+58=2\left(\sqrt[]{1421}+29\right)\left(cm\right)\)

a: Xét ΔABC vuông tại A có BC^2=AB^2+AC^2
=>BC^2=5^2+12^2=169
=>BC=13(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot13=5\cdot12=60\)
=>AH=60/13(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AB^2=BH\cdot BC\)
=>\(BH=\dfrac{AB^2}{BC}=\dfrac{5^2}{13}=\dfrac{25}{13}\left(cm\right)\)
Xét ΔAHB vuông tại H có
\(sinBAH=\dfrac{BH}{AB}=\dfrac{25}{13}:5=\dfrac{5}{13}\)
=>\(\widehat{BAH}\simeq22^0\)
b: HB=HD
=>HD=25/13(cm)
BD=25/13*2=50/13(cm)
BD+DC=BC
=>DC=BC-BD=13-50/13=119/13(cm)
=>R=DC/2=119/26(cm)
c: Xét (O) có
ΔCMD nội tiếp
CD là đường kính
Do đó: ΔCMD vuông tại M
Xét ΔABD có
AH vừa là đường cao, vừa là đường trung tuyến
Do đó: ΔABD cân tại A
=>AB=AD
Xét tứ giác AHDM có
\(\widehat{AHD}+\widehat{AMD}=180^0\)
=>AHDM là tứ giác nội tiếp
=>\(\widehat{ADH}=\widehat{AMH}=\widehat{ABD}\)
ΔAMD vuông tại M
=>AM<AD
mà AD=BA
nên AM<AB
d: \(DM\perp AC;AB\perp AC\Leftrightarrow\)DM//AB
=>\(\widehat{MDA}=\widehat{DAB}\)
=>\(\widehat{MDA}=2\cdot\widehat{DAH}\)


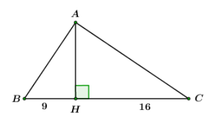
Ta có: BC = BH + CH = 9 + 16 = 25
Áp dụng hệ thức lượng cho ABC vuông tại A có đường cao AH ta có:
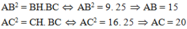
Xét ABC vuông tại A ta có:
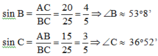
Đáp án cần chọn là: A
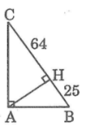
Đáp án C
Ta có: BC = HB + HC = 25 + 64 = 89 cm
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ta có: