
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





2:
a: 5/x-y/3=1/6
=>\(\dfrac{15-xy}{3x}=\dfrac{1}{6}\)
=>\(\dfrac{30-2xy}{6x}=\dfrac{x}{6x}\)
=>30-2xy=x
=>x(2y+1)=30
=>(x;2y+1) thuộc {(30;1); (-30;-1); (10;3); (-10;-3); (6;5); (-6;-5)}
=>(x,y) thuộc {(30;0); (-30;-1); (10;1); (-10;-2); (6;2); (-6;-3)}
b: x/6-2/y=1/30
=>\(\dfrac{xy-12}{6y}=\dfrac{1}{30}\)
=>\(\dfrac{5xy-60}{30y}=\dfrac{y}{30y}\)
=>5xy-60=y
=>y(5x-1)=60
=>(5x-1;y) thuộc {(-1;-60); (4;15); (-6;-10)}(Vì x,y là số nguyên)
=>(x,y) thuộc {(0;-60); (1;15); (-1;-10)}

ĐKXĐ: x<>-1
Đặt \(P=\dfrac{6}{x+1}\cdot\dfrac{x-1}{3}\)
\(P=\dfrac{6}{x+1}\cdot\dfrac{x-1}{3}=\dfrac{6\left(x-1\right)}{3\left(x+1\right)}=\dfrac{2\left(x-1\right)}{x+1}=\dfrac{2x-2}{x+1}\)
Để P là số nguyên thì \(2x-2⋮x+1\)
=>\(2x+2-4⋮x+1\)
=>\(-4⋮x+1\)
=>\(x+1\inƯ\left(-4\right)\)
=>\(x+1\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(x\in\left\{0;-2;1;-3;3;-5\right\}\)

Giup mình với ah.
1- Tính :
A= 5. | x- 5 | - 3x + 1
2 - Tìm các số nguyên x,y ; sao cho :
a) 5/x - y/3 = 1/6 b) 5/x + y/4 = 1/8
3- Tìm giá trị lớn nhất của Q = 27-2x/12-x ( x là số nguyên)
---------------------------------------------------------------------------------------------

1) \(A=5.\left|x-5\right|-3x+1\)
\(A=\left[{}\begin{matrix}5.\left(x-5\right)-3x+1\left(x-5\ge0\right)\\5.\left(5-x\right)-3x+1\left(x-5< 0\right)\end{matrix}\right.\)
\(A=\left[{}\begin{matrix}5x-25-3x+1\left(x\ge5\right)\\25-5x-3x+1\left(x< 5\right)\end{matrix}\right.\)
\(A=\left[{}\begin{matrix}2x-24\left(x\ge5\right)\\26-8x\left(x< 5\right)\end{matrix}\right.\)
3:
\(Q=\dfrac{27-2x}{12-x}=\dfrac{2x-27}{x-12}\)
\(\Leftrightarrow Q=\dfrac{2x-24-3}{x-12}=2-\dfrac{3}{x-12}\)
Để Q lớn nhất thì \(2-\dfrac{3}{x-12}\) lớn nhất
=>\(\dfrac{3}{x-12}\) nhỏ nhất
=>x-12 là số nguyên âm lớn nhất
=>x-12=-1
=>x=11
Vậy: \(Q_{min}=2-\dfrac{3}{11-12}=2+3=5\) khi x=11
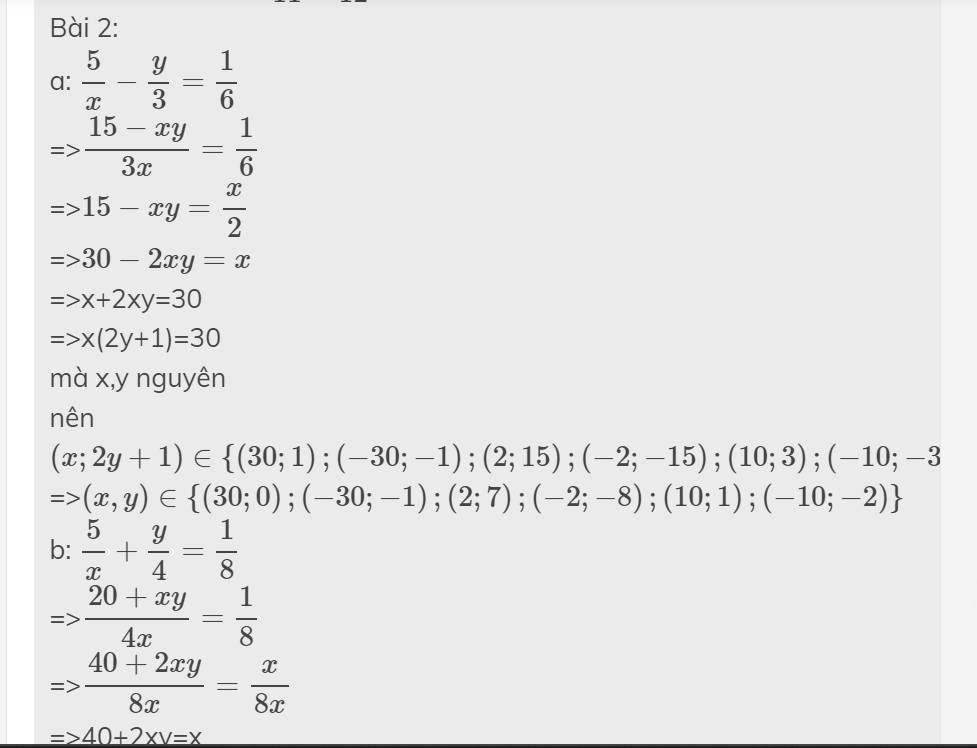
Bài 2:
a: \(\dfrac{5}{x}-\dfrac{y}{3}=\dfrac{1}{6}\)
=>\(\dfrac{15-xy}{3x}=\dfrac{1}{6}\)
=>\(15-xy=\dfrac{x}{2}\)
=>\(30-2xy=x\)
=>x+2xy=30
=>x(2y+1)=30
mà x,y nguyên
nên \(\left(x;2y+1\right)\in\left\{\left(30;1\right);\left(-30;-1\right);\left(2;15\right);\left(-2;-15\right);\left(10;3\right);\left(-10;-3\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(30;0\right);\left(-30;-1\right);\left(2;7\right);\left(-2;-8\right);\left(10;1\right);\left(-10;-2\right)\right\}\)
b: \(\dfrac{5}{x}+\dfrac{y}{4}=\dfrac{1}{8}\)
=>\(\dfrac{20+xy}{4x}=\dfrac{1}{8}\)
=>\(\dfrac{40+2xy}{8x}=\dfrac{x}{8x}\)
=>40+2xy=x
=>x-2xy=40
=>x(1-2y)=40
mà x,y nguyên
nên \(\left(x;1-2y\right)\in\left\{\left(40;1\right);\left(-40;-1\right);\left(8;5\right);\left(-8;-5\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(40;0\right);\left(-40;1\right);\left(8;-2\right);\left(-8;3\right)\right\}\)

`Answer:`
\(x+y=x.y+6\)
\(\Leftrightarrow x+y-xy-6=0\)
\(\Leftrightarrow\left(x-xy\right)+y-6=0\)
\(\Leftrightarrow x\left(1-y\right)+y-1-5=0\)
\(\Leftrightarrow x\left(1-y\right)-\left(1-y\right)=5\)
\(\Leftrightarrow\left(x-1\right)\left(1-y\right)=5\)
Ta có: \(5=\left(-5\right).\left(-1\right)=\left(-1\right).\left(-5\right)=5.1=1.5\)
Ta có bảng sau:
| x - 1 | 5 | -5 | 1 | -1 |
| 1 - y | 1 | -1 | 5 | -5 |
| x | 6 | -4 | 2 | 0 |
| y | 0 | 2 | -4 | 6 |
Vậy `(x;y)\in{(6;0),(4;2),(2;-4),(0;6)}`
x+y=x.y+6 => x.y+6-x-y=0 => x.y-x+6-y=0 => x(y-1)+1-y+5 = 0 => x(y-1) -(y-1) = -5 =>(x-1)(y-1) = -5
Rồi tính tiếp ra các cặp (x;y) : (2;-4), (6;0), (0;6), (-4;2)


\(\frac{5}{x}-\frac{y}{3}=\frac{1}{6}\)
\(\frac{5}{x}=\frac{1}{6}+\frac{2y}{6}=\frac{2y+1}{6}\)
\(\left(2y+1\right)x=30\)
\(\Rightarrow2y+1;x\in\left(1;-1;2;-2;3;-3;5;-5;6;-6;10;-10;-15;15;30;-30\right)\)
Vì 2y + 1 lẻ
\(\Rightarrow2y+1\in\left(1;-1;-3;3;-5;5;-15;15\right)\Rightarrow y\in\left(0;-1;-2;1;-3;2;-8;7\right)\)
\(\Rightarrow x\in\left(30;-30;-10;10;-6;6;-2;2\right)\)
Ta có: \(\frac{5}{x}-\frac{y}{3}=\frac{1}{6}\)
\(\Rightarrow\frac{5}{x}=\frac{1}{6}+\frac{y}{3}\)
\(\Rightarrow\frac{5}{x}=\frac{1}{6}+\frac{2y}{6}=\frac{2y+1}{6}\)
\(\Rightarrow x\left(2y+1\right)=5.6=30\)
\(\Rightarrow x\inƯ(30)\)
Vậy các cặp số nguyên ( x; y ) tương ứng là : ( -2; -8 ); ( 2; 7 ); ( -6; -3 ); ( 6; 2 ); ( -10; -2 ); ( 10; 1 ); ( - 30; -1 ); ( 30; 0 )