Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(\left\{{}\begin{matrix}x=4+2t\\y=1-5t\end{matrix}\right.\)
Vậy: VTCP là (2;-5) và điểm mà (d1) đi qua là A(4;1)
=>VTPT là (5;2)
Phương trình đường thẳng của (d1) là:
5(x-4)+2(y-1)=0
=>5x-20+2y-2=0
=>5x+2y-22=0
(d2): 2x-5y-14=0
=>(d1) và (d2) vuông góc
Xét Δ và d1, hệ phương trình: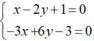 
có vô số nghiệm (do các hệ số của chúng tỉ lệ nên Δ ≡ d1.
Xét Δ và d2, hệ phương trình: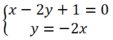 
có nghiệm duy nhất (-1/5; 2/5) nên
Δ cắt d2 tại điểm M(-1/5; 2/5).
Xét Δ và d3, hệ phương trình: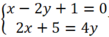 
vô nghiệm
Vậy Δ // d3
Hai đường thẳng song song khi m 3 = 2 − 4 ≠ − 3 2 n ê n m = − 3 2
Chọn đáp án C.
a: Để hai đường cắt nhau thì 1/m<>m/4
=>m2<>4
hay \(m\notin\left\{2;-2\right\}\)
b: Để hai đường song song thì 1/m=m/4
hay \(m\in\left\{2;-2\right\}\)
Do \(\dfrac{1}{-3}=\dfrac{-2}{6}\ne\dfrac{1}{-10}\) nên 2 đường thẳng đã cho song song
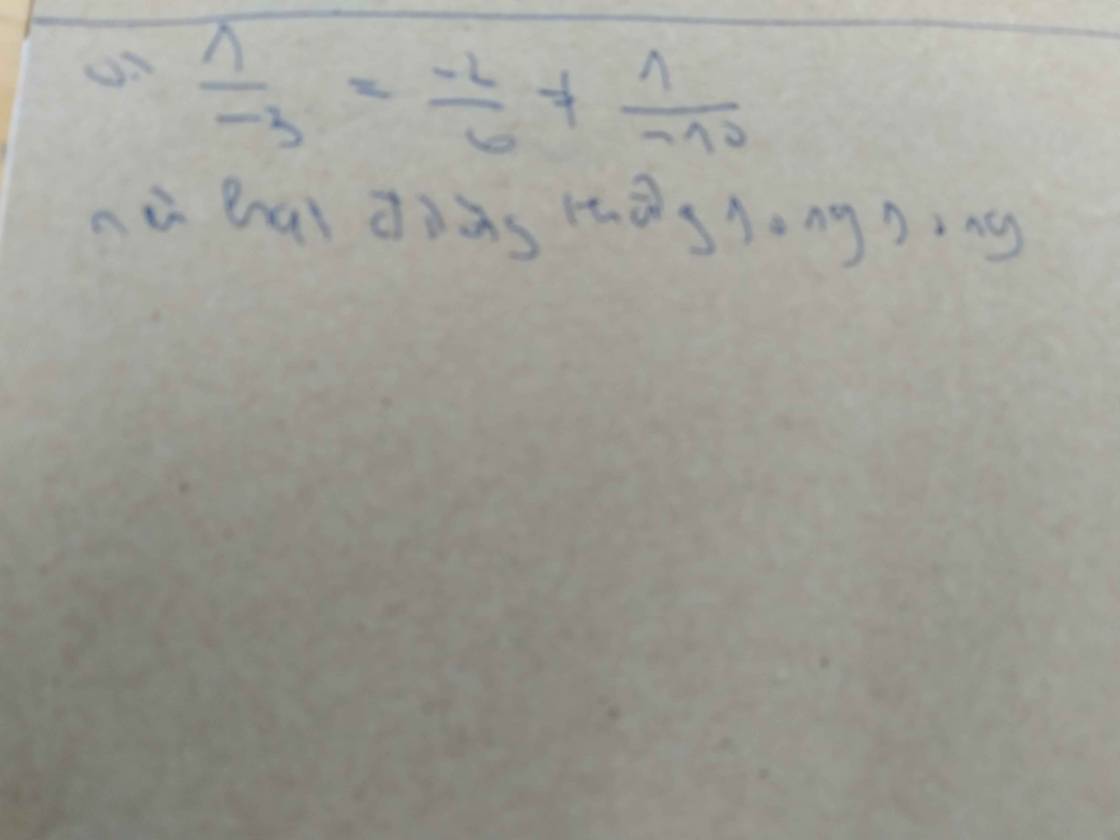
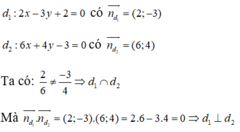
Đường thẳng (d1) có vtpt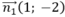
và
d2 có vtpt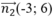
Hai đường thẳng này có
Chọn A.