\(\left\{{}\begin{matrix}x=4+2t\\y=1-5t\end{matrix}\right.\)

Vậy: VTCP là (2;-5) và điểm mà (d1) đi qua là A(4;1)

=>VTPT là (5;2)

Phương trình đường thẳng của (d1) là:

5(x-4)+2(y-1)=0

=>5x-20+2y-2=0

=>5x+2y-22=0

(d2): 2x-5y-14=0

=>(d1) và (d2) vuông góc

Do 4 đỉnh hình vuông nằm trên 2 đường thẳng song song nên độ dài cạnh hình vuông chính là khoảng cách giữa hai đường thẳng song song

Ta có: d2: - x + 2y + 10= 0 hay 2x – 4y – 20 = 0

Khoảng cách hai đường thẳng là: d ( d 1 ; d 2 ) ​ =    1 − ( − 20 ) 2 2 + ​ ( − 4 ) 2 = 21 20

Diện  tích hình  vuông cần  tính  là:   S = 21 20 2 = 441 20

ĐÁP ÁN D.

Giao điểm A của d1 và d2 là nghiệm của hệ:

\(\left\{{}\begin{matrix}x-2y+5=0\\2x-3y+7=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\) \(\Rightarrow A\left(1;3\right)\)

Do \(d//d_3\Rightarrow d\) nhận \(\overrightarrow{n_d}=\left(3;4\right)\) là 1 vtpt

Phương trình d:

\(3\left(x-1\right)+4\left(y-3\right)=0\Leftrightarrow3x+4y-15=0\)

Xét Δ và d1, hệ phương trình: 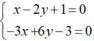 có vô số nghiệm (do các hệ số của chúng tỉ lệ nên Δ ≡ d1.

Xét Δ và d2, hệ phương trình: 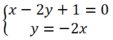 có nghiệm duy nhất (-1/5; 2/5) nên

Δ cắt d2 tại điểm M(-1/5; 2/5).

Xét Δ và d3, hệ phương trình: 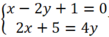vô nghiệm

Vậy Δ // d3

Đường thẳng (d₁)  có vtpt  và

d₂ có vtpt

Hai đường thẳng này có

 nên hai đường thẳng này song song với nhau.

Chọn A.

Hai đường thẳng song song khi  m 3 = 2 − 4 ≠ − 3 2   n ê n   m =   − 3 2

Chọn đáp án C.

a: Để hai đường cắt nhau thì 1/m<>m/4

=>m²<>4

hay \(m\notin\left\{2;-2\right\}\)

b: Để hai đường song song thì 1/m=m/4

hay \(m\in\left\{2;-2\right\}\)