Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b) Phương trình hoành độ giao điểm của (P) và (d) là:
- x 2 = 2mx - 5 ⇔ x 2 + 2mx - 5 = 0
Δ'= m 2 + 5 > 0 với ∀m ∈ R
Vậy trên mặt phẳng Oxy đường thẳng (d) và Parabol (P) luôn cắt nhau tại hai điểm phân biệt.
Khi m = 2, phương trình hoành độ giao điểm của (P) và (d) là:
- x 2 = 4x - 5 ⇔ x 2 + 4x - 5 = 0
Δ = 4 2 - 4.1.(-5) = 36
⇒ Phương trình có 2 nghiệm
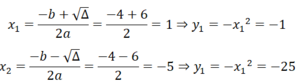
Vậy tọa độ hai giao điểm là M(1;-1) và N(-5;-25)

Xét phương trình hoành độ giao điểm
\(\dfrac{1}{2}x^2=3m-2\) (Với m là tham số)
\(\Leftrightarrow\dfrac{1}{2}x^2-3m+2=0\) (*)
Ta có: \(\Delta=6-4m\)
Để (d) cắt (P) tại 2 điểm phân biệt \(\Leftrightarrow\) Phương trình (*) có 2 nghiệm phân biệt
\(\Leftrightarrow\Delta=6-4m>0\) \(\Leftrightarrow m< \dfrac{3}{2}\)
Vậy ...

Lời giải:
PT hoành độ giao điểm:
$x^2-2mx-(2m+1)=0(*)$
Để (P) và (d) cắt nhau tại 2 điểm pb có hoành độ $x_1,x_2$ thì PT $(*)$ phải có 2 nghiệm pb $x_1,x_2$
$\Leftrightarrow \Delta'=m^2+2m+1>0\Leftrightarrow (m+1)^2>0$
$\Leftrightarrow m\neq -1$
Áp dụng định lý Viet: $x_1+x_2=2m; x_1x_2=-(2m+1)$
Khi đó:
$\sqrt{x_1+x_2}+\sqrt{3+x_1x_2}=2m+1$
$\Leftrightarrow \sqrt{2m}+\sqrt{3-2m-1}=2m+1$
\(\Leftrightarrow \left\{\begin{matrix}
0\leq m< 1\\
\sqrt{2m}+\sqrt{2(1-m)}=2m+1\end{matrix}\right.\)
Bình phương 2 vế dễ dàng giải ra $m=\frac{1}{2}$ (thỏa)

a: PTHĐGĐ là:
x^2-2x-|m|-1=0
a*c=-|m|-1<0
=>(d)luôn cắt (P) tại hai điểm phân biệt
b: Bạn bổ sung lại đề đi bạn

a: Phương trình hoành độ giao điểm là:
\(x^2=2mx-m^2+4\)
=>\(x^2-2mx+m^2-4=0\)
\(\Delta=\left(-2m\right)^2-4\left(m^2-4\right)=4m^2-4m^2+16=16>0\)
=>(P) luôn cắt (d) tại hai điểm phân biệt
b: Theo Vi-et, ta có: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=m^2-4\end{matrix}\right.\)
Sửa đề: \(x_1^2-3x_1+x_2^2-3x_2=4\)
=>\(\left(x_1^2+x_2^2\right)-3\left(x_1+x_2\right)=4\)
=>\(\left(x_1+x_2\right)^2-2x_1x_2-3\left(x_1+x_2\right)=4\)
=>\(\left(2m\right)^2-2\cdot\left(m^2-4\right)-3\cdot2m=4\)
=>\(4m^2-2m^2+8-6m-4=0\)
=>\(2m^2-6m+4=0\)
=>\(m^2-3m+2=0\)
=>(m-1)(m-2)=0
=>\(\left[{}\begin{matrix}m-1=0\\m-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=1\\m=2\end{matrix}\right.\)
Pt hoành độ giao điểm :
2x^2 - 2mx + m - 1 = 0
∆ = (-2m)^2 - 4.2.(m-1)
= 4m^2 - 8m + 4
= ( 2m - 2 ) ^2 > 0 mọi m
=> Pt luôn cắt nhau tại 2 điểm phân biệt.