
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Goi ƯCLN(2n+1;3n+1) là d
=> \(3\left(2n+1\right)-2\left(3n+1\right)\) chia hết cho d
=> \(6n+3-6n-2\) chia hết cho d
=> 1 chia d
=> d\(\inƯ_{\left(1\right)}\)
=> d=1 ; d= - 1
Mà d lớn nhất
=> d=1
Đặt UCLN (2n+1 và 3n+1)=d
\(\Rightarrow\) 2n+1 chia hết cho d và 3n+1 chia hết cho d
\(\Rightarrow\) 6n+3 chia hết cho d và 6n+2 chia hết cho d
\(\Rightarrow\) 1 chia hết cho d
\(\Rightarrow\) d=1 \(\Rightarrow\)ƯCLN (2n+1 và 3n+1)=1![]()


a) Ta có: $(3n+2,5n+3)=(3n+2,2n+1)=(n+1,2n+1)=(n+1,n)=1$.
Các câu sau chứng minh tương tự.

Bài 2:
a: Để E là số nguyên thì \(3n+5⋮n+7\)
\(\Leftrightarrow3n+21-16⋮n+7\)
\(\Leftrightarrow n+7\in\left\{1;-1;2;-2;4;-4;8;-8;16;-16\right\}\)
hay \(n\in\left\{-6;-8;-5;-9;-3;-11;1;-15;9;-23\right\}\)
b: Để F là số nguyên thì \(2n+9⋮n-5\)
\(\Leftrightarrow2n-10+19⋮n-5\)
\(\Leftrightarrow n-5\in\left\{1;-1;19;-19\right\}\)
hay \(n\in\left\{6;4;29;-14\right\}\)

a,
Gọi \(d=ƯC\left(n+1;2n+3\right)\) với \(d\in N\)
\(\Rightarrow\left\{{}\begin{matrix}n+1⋮d\\2n+3⋮d\end{matrix}\right.\) \(\Rightarrow2n+3-2\left(n+1\right)⋮d\)
\(\Rightarrow1⋮d\Rightarrow d=1\)
\(\Rightarrow n+1\) và \(2n+3\) nguyên tố cùng nhau với mọi \(n\in N\)
Các câu sau em biến đổi tương tự

a, n+6 ⋮ n+2 => (n+2)+4 ⋮ n+2
=> 4 ⋮ n+2
=> n ∈ {0;2}
b, 2n+3 ⋮ n - 2
=> 2.(n - 2)+7 ⋮ n - 2
=> 7 ⋮ n - 2
=> n ∈ {3;9}
c, 3n - 1 ⋮ 3 - 2n
=> 2.(3n - 1) ⋮ 3 - 2n
=> 6n - 2 ⋮ 3 - 2n
Ta có: 3(3 - 2n) ⋮ 3 - 2n => 9 - 6n ⋮ 3 - 2n
Do đó: (6n - 2)+(9 - 6n) ⋮ 3 - 2n
=> 7 ⋮ 3 - 2n => n ∈ {1}
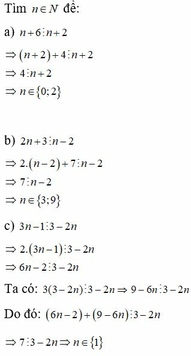
=>6n+2 chia hết cho 2n+3
=>6n+9-7 chia hết cho 2n+3
=>2n+3 thuộc Ư(-7)
mà n là số tự nhiên
nên 2n+3=7
=>2n=4
=>n=2